Signal Processing Basics (Signal Processing Toolbox)

Signal Processing Toolbox

Frequency Response

The Signal Processing Toolbox enables you to perform frequency domain analysis of both analog and digital filters.

Digital Domain

freqz uses an FFT-based algorithm to calculate the z-transform frequency response of a digital filter. Specifically, the statement

```
[h,w] = freqz(b,a,p)
```

returns the p-point complex frequency response, 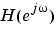, of the digital filter.

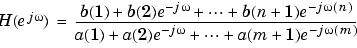
In its simplest form, freqz accepts the filter coefficient vectors b and a, and an integer p specifying the number of points at which to calculate the frequency response. freqz returns the complex frequency response in vector h, and the actual frequency points in vector w in rad/s.

freqz can accept other parameters, such as a sampling frequency or a vector of arbitrary frequency points. The example below finds the 256-point frequency response for a 12th-order Chebyshev Type I filter. The call to freqz specifies a sampling frequency fs of 1000 Hz:

[b,a] = cheby1(12,0.5,200/500);
[h,f] = freqz(b,a,256,1000);

Because the parameter list includes a sampling frequency, freqz returns a vector f that contains the 256 frequency points between 0 and fs/2 used in the frequency response calculation.

Note This toolbox uses the convention that unit frequency is the Nyquist frequency, defined as half the sampling frequency. The cutoff frequency parameter for all basic filter design functions is normalized by the Nyquist frequency. For a system with a 1000 Hz sampling frequency, for example, 300 Hz is 300/500 = 0.6. To convert normalized frequency to angular frequency around the unit circle, multiply by

. To convert normalized frequency back to hertz, multiply by half the sample frequency.

If you call freqz with no output arguments, it plots both magnitude versus frequency and phase versus frequency. For example, a ninth-order Butterworth lowpass filter with a cutoff frequency of 400 Hz, based on a 2000 Hz sampling frequency, is

```
[b,a] = butter(9,400/1000);
```

To calculate the 256-point complex frequency response for this filter, and plot the magnitude and phase with freqz, use

```
freqz(b,a,256,2000)
```

or to display the magnitude and phase responses in fvtool, which provides additional analysis tools, use

```
fvtool(b,a)
```

and click the Magnitude and Phase Response button on the toolbar:

freqz can also accept a vector of arbitrary frequency points for use in the frequency response calculation. For example,

```
w = linspace(0,pi);
h = freqz(b,a,w);
```

calculates the complex frequency response at the frequency points in w for the filter defined by vectors b and a. The frequency points can range from 0 to 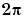. To specify a frequency vector that ranges from zero to your sampling frequency, include both the frequency vector and the sampling frequency value in the parameter list.

Impulse Response Analog Domain