Optimization Toolbox

Nonlinear Minimization with Gradient and Hessian

This example involves solving a nonlinear minimization problem with a tridiagonal Hessian matrix H(x) first computed explicitly, and then by providing the Hessian's sparsity structure for the finite-differencing routine.

The problem is to find x to minimize

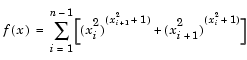
(2-7)

where n = 1000.

Step 1: Write an M-file brownfgh.m that computes the objective function, the gradient of the objective, and the sparse tridiagonal Hessian matrix.

This file is rather long and is not included here. You can view the code with the command

• type brownfgh
  

Because brownfgh computes the gradient and Hessian values as well as the objective function, you need to use optimset to indicate that this information is available in brownfgh, using the GradObj and Hessian parameters.

Step 2: Call a nonlinear minimization routine with a starting point xstart.

• n = 1000;
  xstart = -ones(n,1); 
  xstart(2:2:n,1) = 1;
  options = optimset('GradObj','on','Hessian','on');
  [x,fval,exitflag,output] = fminunc(@brownfgh,xstart,options); 
  

This 1000 variable problem is solved in 8 iterations and 7 conjugate gradient iterations with a positive exitflag indicating convergence. The final function value and measure of optimality at the solution x are both close to zero. For fminunc, the first order optimality is the infinity norm of the gradient of the function, which is zero at a local minimum:

• exitflag =
       1
  fval =
    2.8709e-017
  output.iterations
  ans =
       8
  output.cgiterations
  ans =
       7
  output.firstorderopt
  ans =
    4.7948e-010
  

Nonlinear Least-Squares with Full Jacobian Sparsity Pattern

Nonlinear Minimization with Gradient and Hessian Sparsity Pattern