System Identification Toolbox

zpkdata

Compute zeros, poles, and transfer function gains of models.

Syntax

• [z,p,k] = zpkdata(m)
  [z,p,k,dz,dp,dk] = zpkdata(m)
  [z,p,k,dz,dp,dk] = zpkdata(m,'v')
  

Description

m is a model given as any idmodel object with ny output channels and nu input channels.

z is a a cell array of dimension ny-by-nu. z{ky,ku} (note the curly brackets) contains the zeros of the transfer function from input ku to output ky. This is a column vector of possibly complex numbers.

Similarily p is an ny-by-nu cell array containing the poles.

k is a ny-by-nu matrix whose ky-ku entry is the transfer function gain of the transfer function from input ku to output ky. Note that the transfer function gain is value of the leading coefficient of the numerator, when the leading coefficient of the denominator is normalized to 1. It thus differs from the static gain. The static gain can be retrieved as Ks = freqresp(m,0).

dz contains the covariance matrices of the zeros in the following way: dz is a ny-by-nu cell array. dz{ky,ku} contains the covariance information about the zeros of the transfer function from ku to ky. It is a 3-D array of dimension 2-by-2-by-Nz, where Nz is the number of zeros. dz{ky,ku}(:,:,kz) is the covariance matrix of the zero z{ky,ku}(kz), so that the 1-1 element is the variance of the real part, the 2-2 element is the variance of the imaginary part and the 1-2 and 2-1 elements contain the covariance between the real and imaginary parts.

dp contains the covariance matrices of the poles in the same way.

dk is a matrix containing the variances of the elements of k.

If m is a SISO model, adding an extra input argument 'v' (for vector) will return z and p as vectors rather than cell arrays.

Note that the zeros and the poles are associated with the different channels combinations. To obtain the so-called transmission zeros, use tzero.

The noise input channels in m are treated as follows: Consider a model m with both measured input channels u (nu channels) and noise channels e (ny channels) with covariance matrix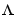

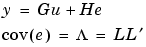
where L is a lower triangular matrix. Note that m.NoiseVariance = 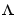. The model can also be described with unit variance, normalized noise source v.

Then:

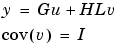
• zpkdata(m) returns the zeros and poles of G.
• zpkdata(m('n')) returns the zeros and poles of H. (ny inputs and ny outputs)
• If m is a time series, that is nu = 0, zpkdata(m) returns the zeros and poles of H.
• zpkdata(noisecnv(m)) returns the zeros and poles of the transfer function [G H] (nu+ny inputs and ny outputs)
• zpkdata(noisecnv(m,'norm')) returns the zeros and poles of the transfer function [G HL] (nu+ny inputs and ny outputs.

The procedure handles both models in continuous and discrete time.

Note that you cannot rely on information about zeros and poles at the origin and at infinity for discrete time models. (This is a somewhat confusing issue anyway.)

Algorithm

The poles and zeros are computed using ss2zp. The covariance information is computed using Gauss's approximation formula, using the parameter covariance matrix contained in m. When the transfer function depends on the parameters in a complicated way, numerical differentiation is applied. The step-sizes for the differentiation are determined in the M-file nuderst.

view