| System Identification Toolbox | |
Available Algorithms
The System Identification Toolbox provides the following functions that implement all common recursive identification algorithms for model structures in the family (3-43): rarmax, rarx, rbj, rpem, rplr, and roe. They all share the following basic syntax.
Here z contains the output-input data as usual. nn specifies the model structure, exactly as for the corresponding offline algorithm. The arguments adm and adg select the adaptation mechanism and adaptation gain listed above.
gives the forgetting factor algorithm (3-62), with forgetting factor lam.
gives the unnormalized gradient approach (3-63) with gain gam. Similarly,
gives the normalized gradient approach (3-64). To obtain the Kalman filter approach (3-60) with drift matrix R1, enter
The value of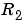 
is always 1. Note that the estimates 
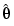in (3-60) are not affected if all the matrices 
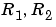and 
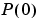are scaled by the same number. You can therefore always scale the original problem so that 
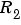becomes 1.
The output argument thm is a matrix that contains the current models at the different samples. Row k of thm contains the model parameters, in alphabetical order at sample time k, corresponding to row k in the data matrix z. The ordering of the parameters is the same as m.par would give when applied to a corresponding offline model.
The output argument yh is a column vector that contains, in row k, the predicted value of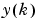 
, based on past observations and current model. The vector yh thus contains the adaptive predictions of the outputs, and is useful also for noise cancelling and other adaptive filtering applications.
The functions also have optional input arguments that allow the specification of 
, and 
. Optional output arguments include the last value of the matrix P and of the vector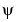 
.
Now, rarx is a recursive variant of arx; similarly rarmax is the recursive counterpart of armax and so on. Note, though that rarx does not handle multi-output systems, and rpem does not handle state-space structures.
The function rplr is a variant of rpem, and uses a different approximation of the gradient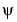 
. It is known as the recursive pseudo-linear regression approach, and contains some well known special cases. See Equation (11.57) in Ljung (1999). When applied to the output error model (nn=[0 nb 0 0 nf nk]) it results in methods known as HARF ('ff'-case) and SHARF ('ng'-case). The common extended least squares (ELS) method is an rplr algorithm for the
ARMAX model (nn=[na nb nc 0 0 nk]).
The following example shows a second order output error model, which is built recursively and its time varying parameter estimates plotted as functions of time.
The next example shows how a second order ARMAX model is recursively estimated by the ELS method, using Kalman filter adaptation. The resulting static gains of the estimated models are then plotted as a function of time.
[N,dum]=size(z); thm = rplr(z,[2 2 2 0 0 1],'kf',0.01*eye(6)); nums = sum(thm(:,3:4)')'; dens = ones(N,1)+sum(thm(:,1:2)')'; stg = nums./dens; plot(stg)
So far, the examples of applications where a batch of data is examined cover studies of the variability of the system. The algorithms are, however, also prepared for true online applications, where the computed model is used for some online decision. This is accomplished by storing the update information in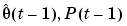 
and information about past data in 
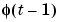(and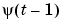 
) and using that information as initial data for the next time step. The following example shows the recursive least squares algorithm being used on line (just to plot one current parameter estimate).
%Initialization, first i/o pair y,u (scalars) [th,yh,P,phi] = rarx([y u],[2 2 1],'ff',0.98); axis([1 50 -2 2]) plot(1,th(1),'*'),hold %The online loop: for k = 2:50 % At time k receive y,u [th,yh,P,phi] = rarx([y u],[2 2 1],'ff',0.98,th',P,phi); plot(k,th(1),'*') end
Execute iddemo #10 to illustrate the recursive algorithms.
| | Choosing an Adaptation Mechanism and Gain | Segmentation of Data | |