Tutorial (System Identification Toolbox)

System Identification Toolbox

Comparing Different Structures

It is natural to compare the results obtained from model structures with different orders. For state-space models this is easily obtained by using a vector argument for the order in n4sid or pem.

m = n4sid(Data,1:10)
m = pem(Data,'nx',3:15)

This invokes a plot from which a "best" order is chosen. Just omitting the order argument, m = n4sid(Data) or pem(Data) makes a default choice of the best order.

For models of ARX type, various orders and delays can be efficiently studied with the command arxstruc. Collect in a matrix NN all of the ARX structures you want to investigate, so that each row of NN is of the type

```
[na nb nk]
```

With

```
V = arxstruc(Date,Datv,NN)
```

an ARX model is fitted to the data set Date for each of the structures in NN. Next, for each of these models, the sum of squared prediction errors is computed, as they are applied to the data set Datv. The resulting loss functions are stored in V together with the corresponding structures.

To select the structure that has the smallest loss function for the validation set Datv, use

```
nn = selstruc(V,0)
```

Such a procedure is known as cross validation and is a good way to approach the model selection problem.

It is usually a good idea to visually inspect how the fit changes with the number of estimated parameters. A graph of the fit versus the number of parameters is obtained with

```
selstruc(V)
```

This routine prompts you to choose the number of parameters to estimate, based upon visual inspection of the graph, and then it selects the structure with the best fit for that number of parameters.

The command struc helps generate typical structure matrices NN for single-input systems. A typical sequence of commands is

V = arxstruc(Date,Datv,struc(2,2,1:10));
nn = selstruc(V,0);
nk = nn(3);
V = arxstruc(Date,Datv,struc(1:5,1:5,nk-1:nk+1));
selstruc(V)

where you first establish a suitable value of the delay nk by testing second order models with delays between one and ten. The best fit selects the delay, and then all combinations of ARX models with up to five a and b parameters are tested with delays around the chosen value (a total of 75 models).

If the model is validated on the same data set from which it was estimated; i.e., if Date = Datv, the fit always improves as the flexibility of the model structure increases. You need to compensate for this automatic decrease of the loss functions. There are several approaches for this. Probably the best known technique is Akaike's Final Prediction Error (FPE) criterion and his closely related Information Theoretic Criterion (AIC). Both simulate the cross validation situation, where the model is tested on another data set.

The FPE is formed as

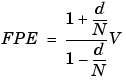
where d is the total number of estimated parameters and N is the length of the data record. V is the loss function (quadratic fit) for the structure in question. The AIC is formed as

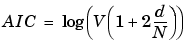
(See Section 16.4 in Ljung (1999).)

According to Akaike's theory, in a collection of different models, choose the one with the smallest FPE (or AIC). The FPE values are displayed with the model parameters, by just typing the model name. It is also one of the fields in EstimationInfo, and can be accessed by

```
FPE = fpe(m)
```

Similarly, the AIC value of an estimated model is obtained as

```
AIC = aic(m)
```

The structure that minimizes the AIC is obtained with

```
nn = selstruc(V,'AIC')
```

where V was generated by arxstruc.

A related criterion is Rissanen's Minimum Description Length (MDL) approach, which selects the structure that allows the shortest over-all description of the observed data. This is obtained with

```
nn = selstruc(V,'MDL')
```

If substantial noise is present, the ARX models may need to be of high order to describe simultaneously the noise characteristics and the system dynamics. (For ARX models the disturbance model 1/A(q) is directly coupled to the dynamics model B(q)/A(q).)

Model Structure Selection and Validation Impulse Response to Determine Delays