System Identification Toolbox

State-Space Models with Coupled Parameters: the idgrey Model

In some situations you may want the unknown parameters in the matrices in (3-51) or (3-52) to be linked to each other. Then the NaN feature is not sufficient to describe these links. Instead you need to do some "greybox" modeling and write an M-file that describes the structure. The format is

• [A,B,C,D,K,x0] = mymfile(par,T,aux);
  

where mymfile is the user-defined name for the M-file, par contains the parameters as a column vector, T is the sampling interval, and aux contains auxiliary variables. The latter variables are used to house options, so that some different cases can be tried out without having to edit the M-file. The matrices A, B, C, D, K, and x0 refer either to the continuous time description (3-52) or to the discrete-time description (3-51). When a continuous time description is fitted to sampled data, the estimation routines perform the necessary sampling of the model. To obtain the same structure as in the Example 3.2, you can do the following.

• function [A,B,C,D,K,x0] = mymfile(par,T,aux)
  A = [0 1; 0 par(1)]; 
  B = [0;par(2)];
  C = eye(2);
  D = zeros(2,2);
  K = zeros(2,1);
  x0 =[par(3);0];
  

Once the M-file has been written, the idgrey model m is defined by the command

• m = idgrey('mymfile',par,'c',aux);
  

where par contains the nominal (initial) values of the corresponding entries in the structure. 'c' signals that the underlying parametrization is continuous time. aux contains the values of the auxiliary parameters. Note that T and aux must be given as input arguments, even if they are not used by the code.

From here on, estimate models and evaluate results as for any other model structure. Some further examples of user-defined model structures are given below.

Some Examples of idgrey Model Structures

With user-defined structures, you have complete freedom in the choice of models of linear systems. This section gives two examples of such structures.

Example 3.3: Heat Diffusion.   Consider a system driven by the heat-diffusion equation (see also Example 4.3 in Ljung (1999)).

This is a metal rod with a heat-diffusion coefficient 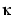, which is insulated at the near end and heated by the power u (W) at the far end. The output of the system is the temperature at the near end. This system is described by a partial differential equation in time and space. Replacing the space-second derivative by a corresponding difference approximation gives a time-continuous state-space model (3-52), where the dimension of x depends on the grid-size in space used in the approximation. It is also desirable to be able to work with different grid sizes without having to edit the model file. This is described by the following M-file.

• function [A,B,C,D,K,x0] = heatd(pars,T,aux)
  Ngrid = aux(1); % Number of points in the space-discretization
  L = aux(2); % Length of the rod
  temp = aux(3); % Assuming uniform initial temperature of the rod
  deltaL = L/Ngrid;    % Space interval
  kappa = pars(1); % The heat-diffusion coefficient
  htf = pars(2); % Heat transfer coefficient at far end of rod
  A = zeros(Ngrid,Ngrid);
  for kk = 2:Ngrid-1
  A(kk,kk-1) = 1;
  A(kk,kk) = -2;
  A(kk,kk+1) = 1;
  end
  A(1,1) = -1; A(1,2) = 1; % Near end of rod insulated
  A(Ngrid,Ngrid-1) = 1;
  A(Ngrid,Ngrid) = -1;
  A = A*kappa/deltaL/deltaL;
  B = zeros(Ngrid,1); 
  B(Ngrid,1) = htf/deltaL;
  C = zeros(1,Ngrid);
  C(1,1) = 1;
  D = 0;
  K = zeros(Ngrid,1);
  x0 = temp*ones(Ngrid,1);
  

You can then define the model by

• m = idgrey('heatd',[0.27 1],'c',[10,1,22])
  

for a 10th order approximation of a heat rod one meter in length, with an initial temperature of 22 degrees. The initial estimate of the heat conductivity is 0.27, and of the heat transfer coefficient is 1.

The model parameters are estimated by

• me = pem(Data,m)
  

If you would like to try a finer grid, that is, take Ngrid larger, you can do this easily with

• me = pem(Data,m,'Filearg',[20,1,22])
  

Example 3.4: Parametrized Disturbance Models.   Consider a discrete-time model

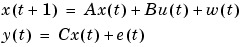
where w and e are independent white noises with covariance matrices R1 and R2, respectively. Suppose that you know the variance of the measurement noise R2, and that only the first component of 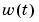is nonzero. This can be handled by the following M-file.

• function [A,B,C,D,K,x0] = mynoise(par,T,aux)
  R2 = aux(1); % The assumed known measurement noise variance
  A = [par(1) par(2);1 0];
  B = [1;0];
  C = [par(3) par(4)];
  D = 0;
  R1 = [par(5) 0;0 0];
  K = A*dlqe(A,eye(2),C,R1,R2); % from the Control System Toolbox
  x0 = [0;0];
  

Structured State-Space Models with Free Parameters: the idss Model

State-Space Structures: Initial Values and Numerical Derivatives