Fixed-Point Blockset

Parallel Form

In the canonical parallel form, the transfer function H(z) is expanded into partial fractions. H(z) is then realized as a sum of a constant, first-order, and second-order transfer functions, as shown:

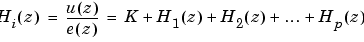
This expansion, where K is a constant and the 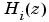are the first and second-order transfer functions, follows.

As in the series canonical form, there is no unique description for the first-order and second-order transfer function. Due to the nature of the Sum block, the ordering of the individual filters doesn't matter. However, because of the constant K, you can choose the first-order and second-order transfer functions such that their forms are simpler than those for the series cascade form described in the preceding section. This is done by expanding H(z) as

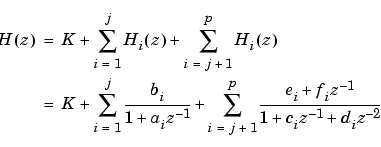
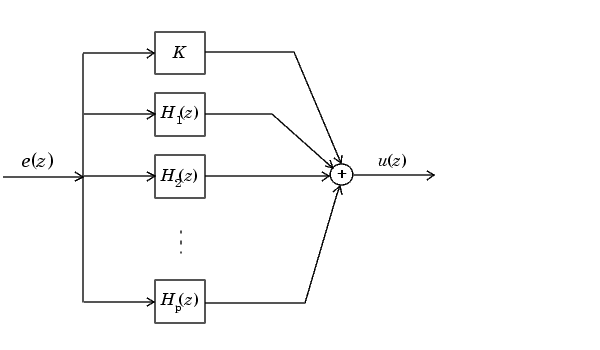
The first order diagram for H(z) follows.

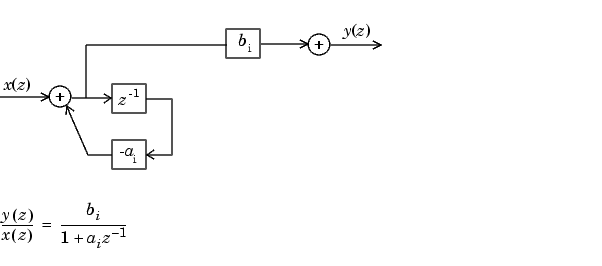
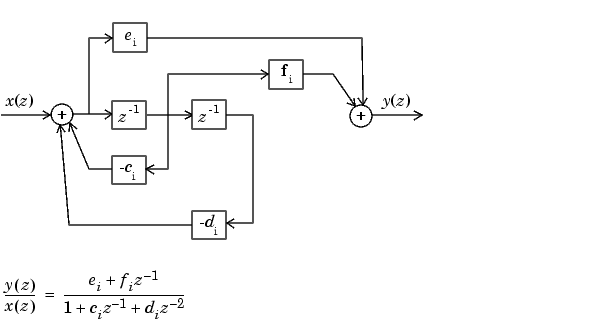
The second order diagram for H(z) follows.

The parallel form example transfer function is given by

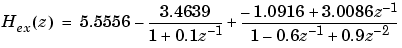
The realization of H_ex(z) using the Fixed-Point Blockset is shown below. You can display this model by typing

• fxpdemo_parallel_form
  

at the MATLAB command line.

Series Cascade Form

Tutorial: Feedback Controller Simulation