Data Types and Scaling (Fixed-Point Blockset)

Fixed-Point Blockset

Range and Precision

The range of a number gives the limits of the representation while the precision gives the distance between successive numbers in the representation. The range and precision of a fixed-point number depends on the length of the word and the scaling.

Range

The range of representable numbers for an unsigned and two's complement fixed-point number of size ws, scaling S, and bias B is illustrated below.

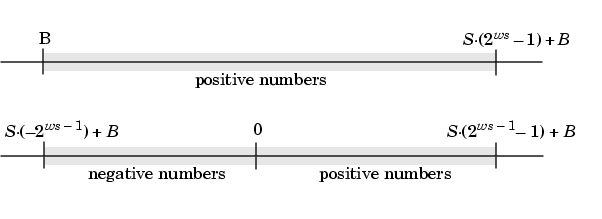
For both the signed and unsigned fixed-point numbers of any data type, the number of different bit patterns is 2^ws.

For example, if the fixed-point data type is an integer with scaling defined as S = 1 and B = 0, then the maximum unsigned value is 2^ws- 1 since zero must be represented. In two's complement, negative numbers must be represented as well as zero so the maximum value is 2^{ws -}¹- 1. Additionally, since there is only one representation for zero, there must be an unequal number of positive and negative numbers. This means there is a representation for -2^{ws -}¹but not for 2^{ws -}¹.

Precision

The precision (scaling) of integer and fractional data types is specified by the default radix point. For generalized fixed-point data types, the scaling must be explicitly defined as either [Slope Bias] or radix point-only. In either case, the precision is given by the slope.

Fixed-Point Data Type Parameters

The low limit, high limit, and default radix point-only scaling for the supported fixed-point data types discussed in Radix Point Interpretation are given below. See Limitations on Precision and Limitations on Range for more information.

Fixed-Point Data Type Range and Default Scaling
Name
Data Type
Low Limit
High Limit
Default Scaling (~Precision)

Integer
uint
0
2^ws - 1
1

sint
-2^ws^{- 1}
2^ws^{- 1} - 1
1

Fractional
ufrac
0
1 - 2^-ws
2^-ws

sfrac
-1
1 - 2^-⁽^ws^{- 1)}
2^-⁽^ws^{- 1)}

Generalized Fixed-Point
ufix
N/A
N/A
N/A

sfix
N/A
N/A
N/A

**Fixed-Point Data Type Range and Default Scaling**
Name	Data Type	Low Limit	High Limit	Default Scaling (~Precision)
Integer	`uint`	0	2^ws - 1	1
`sint`	-2^ws^{- 1}	2^ws^{- 1} - 1	1
Fractional	`ufrac`	0	1 - 2^-ws	2^-ws
`sfrac`	-1	1 - 2^-⁽^ws^{- 1)}	2^-⁽^ws^{- 1)}
Generalized Fixed-Point	`ufix`	N/A	N/A	N/A
`sfix`	N/A	N/A	N/A

Quantization Example: Fixed-Point Scaling