

| Fixed-Point Blockset |   |
Example: Selecting a Measurement Scale
On typical electronically controlled internal combustion engines, the flow of fuel is regulated to obtain the desired ratio of air to fuel in the cylinders just prior to combustion. Therefore, knowledge of the current air flow rate is required. Some manufacturers use sensors that directly measure air flow while other manufacturers calculate air flow from measurements of related signals. The relationship of these variables is derived from the ideal gas equation. The ideal gas equation involves division by air temperature. For proper results, an absolute temperature scale such as Kelvin or Rankine must be used in the equation. However, quantization directly to an absolute temperature scale would cause needlessly large quantization errors.
The temperature of the air flowing into the engine has a limited range. On a typical engine, the radiator is designed to keep the block below the boiling point of the cooling fluid. Let's assume a maximum of 225o F (380o K). As the air flows through the intake manifold, it can be heated up to this maximum temperature. For a cold start in an extreme climate, the temperature can be as low as -60o F (222o K). Therefore, using the absolute Kelvin scale, the range of interest is 222o K to 380o K.
The air temperature needs to be quantized for processing by the embedded control system. Assuming an unrealistic quantization to 3-bit unsigned numbers: 0,1,2,...,7, the purely linear conversion with maximum precision is
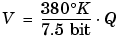
The quantized conversion and range of interest are shown below.
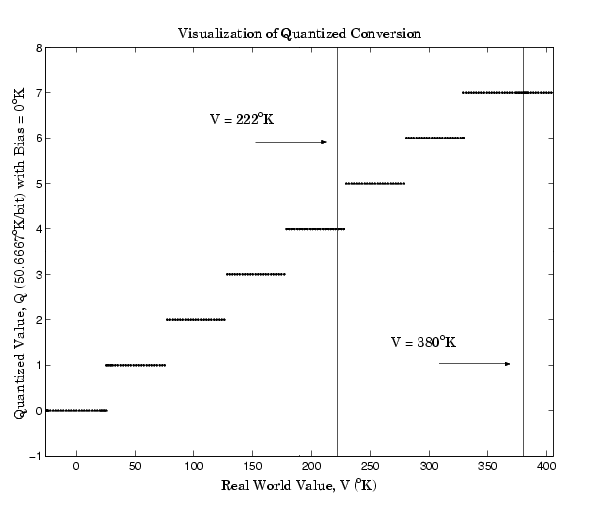
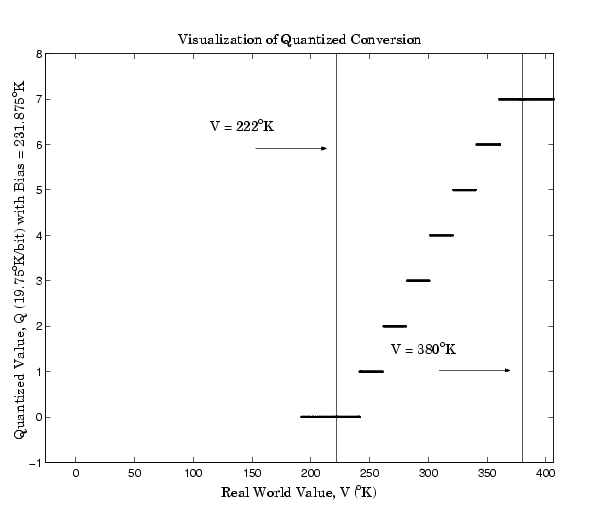
Notice that there are 7.5 possible quantization values. This is because only half of the first bit corresponds to temperatures (real-world values) greater than zero.
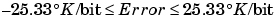
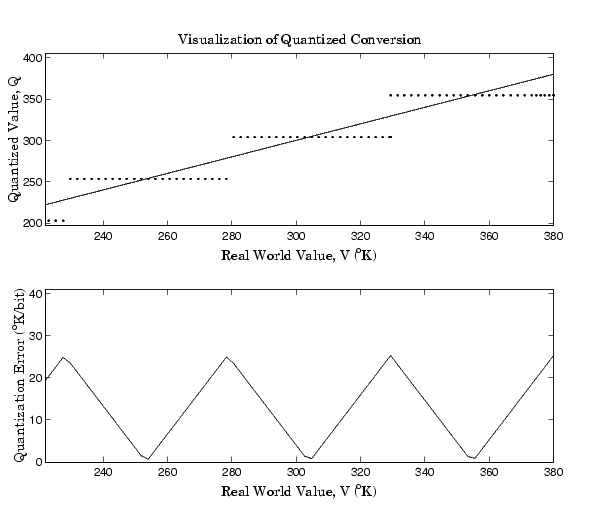
The range of interest of the quantized conversion and the absolute value of the quantized error are shown below.
As an alternative to the purely linear conversion, consider the general linear conversion with maximum precision:
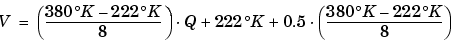
The quantized conversion and range of interest are shown below.
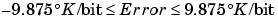
which is approximately 2.5 times smaller than the error associated with the purely linear conversion.
The range of interest of the quantized conversion and the absolute value of the quantized error are shown below.
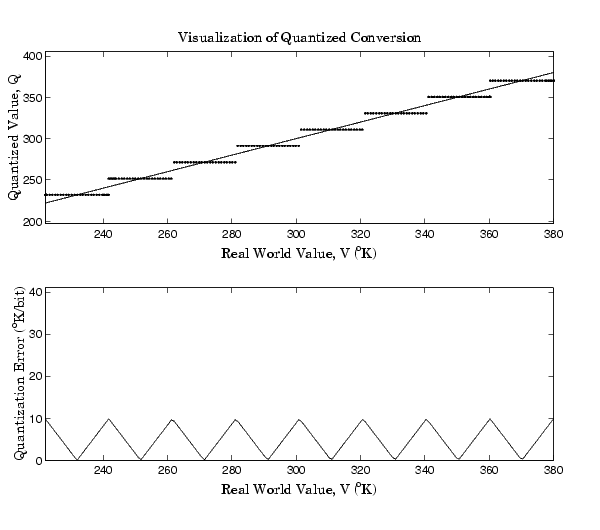
Clearly, the general linear scale gives much better precision than the purely linear scale over the range of interest.
 | Selecting a Measurement Scale | Why Use Fixed-Point Hardware? |  |