Financial Toolbox

Solving Simultaneous Linear Equations

Matrix division is especially useful in solving simultaneous linear equations. Consider this problem: given two portfolios of mortgage-based instruments, each with certain yields depending on the prime rate, how do you weight the portfolios to achieve certain annual cash flows? The answer involves solving two linear equations.

A linear equation is any equation of the form

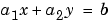
where a₁, a₂, and b are constants (with a₁ and a₂ not both zero), and x and y are variables. (It's a linear equation because it describes a line in the xy-plane. For example the equation 2x + y = 8 describes a line such that if x = 2 then y = 4.)

A system of linear equations is a set of linear equations that we usually want to solve at the same time; i.e., simultaneously. A basic principle for exact answers in solving simultaneous linear equations requires that there be as many equations as there are unknowns. To get exact answers for x and y there must be two equations. For example, to solve for x and y in the system of linear equations

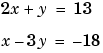
there must be two equations, which there are. Matrix algebra represents this system as an equation involving three matrices: A for the left-side constants, X for the variables, and B for the right-side constants

where A*X = B.

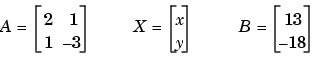
Solving the system simultaneously simply means solving for X. Using MATLAB,

• A = [2  1
       1 -3];
  
  B = [13
      -18];
  

• X = A \ B
  

solves for X in A * X = B.

• X = [3
       7]
  

So x = 3 and y = 7 in this example. In general, you can use matrix algebra to solve any system of linear equations such as

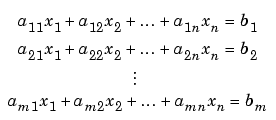
by representing them as matrices

and solving for X in A*X = B.

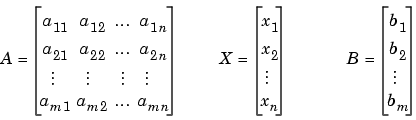
To illustrate, consider this situation. There are two portfolios of mortgage-based instruments, M1 and M2. They have current annual cash payments of $100 and $70 per unit, respectively, based on today's prime rate. If the prime rate moves down one percentage point, their payments would be $80 and $40. An investor holds 10 units of M1 and 20 units of M2. The investor's receipts equal cash payments times units, or R = C * U, for each prime-rate scenario. As word equations,

	M1	M2
Prime flat:	$100 * 10 units	+ $70 * 20 units = $2400 receipts
Prime down:	$80 * 10 units	+ $40 * 20 units = $1600 receipts

As MATLAB matrices

• Cash = [100  70
           80  40];
  
  Units =[10
          20];
  
  Receipts = Cash * Units
  
  Receipts =
  
         2400.00
         1600.00
  

Now the investor asks the question: given these two portfolios and their characteristics, how many units of each should I hold to receive $7000 if the prime rate stays flat and $5000 if the prime drops one percentage point? Find the answer by solving two linear equations.

	M1	M2
Prime flat:	$100 * x units	+ $70 * y units = $7000 receipts
Prime down:	$80 * x units	+ $40 * y units = $5000 receipts

In other words, solve for U (units) in the equation R (receipts) = C (cash) * U (units). Using MATLAB left division

• Cash = [100  70
           80  40];
  
  Receipts = [7000
              5000];
  
  Units = Cash \ Receipts
  Units =
  
           43.75
           37.50
  

The investor should hold 43.75 units of portfolio M1 and 37.5 units of portfolio M2 to achieve the annual receipts desired.

Dividing Matrices

Operating Element-by-Element