Financial Toolbox

Interest Rates/Rates of Return

Several functions calculate interest rates involved with cash flows. To compute the internal rate of return of the cash stream, simply execute the toolbox function irr

• ROR = irr(Stream)
  

which gives a rate of return of 11.72%.

Note that the internal rate of return of a cash flow may not have a unique value. Every time the sign changes in a cash flow, the equation defining irr can give up to two additional answers. An irr computation requires solving a polynomial equation, and the number of real roots of such an equation can depend on the number of sign changes in the coefficients. The equation for internal rate of return is

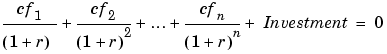
where Investment is a (negative) initial cash outlay at time 0, cf_n is the cash flow in the nth period, and n is the number of periods. Basically, irr finds the rate r such that the net present value of the cash flow equals the initial investment. If all of the cf_ns are positive there is only one solution. Every time there is a change of sign between coefficients, up to two additional real roots are possible. There is usually only one answer that makes sense, but it is possible to get returns of both 5% and 11% (for example) from one income stream.

Another toolbox rate function, effrr, calculates the effective rate of return given an annual interest rate (also known as nominal rate or annual percentage rate, APR) and number of compounding periods per year. To find the effective rate of a 9% APR compounded monthly, simply enter

• Rate = effrr(0.09, 12)
  

The answer is 9.38%.

A companion function nomrr computes the nominal rate of return given the effective annual rate and the number of compounding periods.

Analyzing and Computing Cash Flows

Present or Future Values