balreal (Function Reference)

Input/output balancing of state-space realizations

Syntax

sysb = balreal(sys)
[sysb,g,T,Ti] = balreal(sys)

Description

sysb = balreal(sys) produces a balanced realization sysb of the LTI model sys with equal and diagonal controllability and observability grammians (see gram for a definition of grammian). balreal handles both continuous and discrete systems. If sys is not a state-space model, it is first and automatically converted to state space using ss.

[sysb,g,T,Ti] = balreal(sys) also returns the vector g containing the diagonal of the balanced grammian, the state similarity transformation 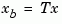used to convert sys to sysb, and the inverse transformation.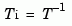

If the system is normalized properly, the diagonal g of the joint grammian can be used to reduce the model order. Because g reflects the combined controllability and observability of individual states of the balanced model, you can delete those states with a small g(i) while retaining the most important input-output characteristics of the original system. Use modred to perform the state elimination.

Example

Consider the zero-pole-gain model

sys = zpk([-10 -20.01],[-5 -9.9 -20.1],1)
 
Zero/pole/gain:
   (s+10) (s+20.01)
----------------------
(s+5) (s+9.9) (s+20.1)

A state-space realization with balanced grammians is obtained by

```
[sysb,g] = balreal(sys)
```

The diagonal entries of the joint grammian are

g'
 
ans =
   1.0062e-01   6.8039e-05   1.0055e-05

which indicates that the last two states of sysb are weakly coupled to the input and output. You can then delete these states by

```
sysr = modred(sysb,[2 3],'del')
```

to obtain the following first-order approximation of the original system.

zpk(sysr)

Zero/pole/gain:
 1.0001
--------
(s+4.97)

Compare the Bode responses of the original and reduced-order models.

```
bode(sys,'-',sysr,'x')
```

Algorithm

Consider the model

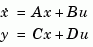
with controllability and observability grammians 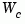and 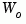. The state coordinate transformation 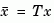produces the equivalent model

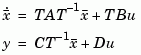
and transforms the grammians to

The function balreal computes a particular similarity transformation 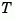such that

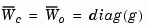
See [1,2] for details on the algorithm.

Limitations

The LTI model sys must be stable. In addition, controllability and observability are required for state-space models.

See Also
gram Controllability and observability grammians

minreal Minimal realizations

modred Model order reduction

References

[1] Laub, A.J., M.T. Heath, C.C. Paige, and R.C. Ward, "Computation of System Balancing Transformations and Other Applications of Simultaneous Diagonalization Algorithms," IEEE Trans. Automatic Control, AC-32 (1987), pp. 115-122.

[2] Moore, B., "Principal Component Analysis in Linear Systems: Controllability, Observability, and Model Reduction," IEEE Transactions on Automatic Control, AC-26 (1981), pp. 17-31.

[3] Laub, A.J., "Computation of Balancing Transformations," Proc. ACC, San Francisco, Vol.1, paper FA8-E, 1980.

augstate bandwidth