Reliable Computations

Scaling

State space is the preferred model for LTI systems, especially with higher order models. Even with state-space models, however, accurate results are not guaranteed, because of the finite-word-length arithmetic of the computer. A well-conditioned problem is usually a prerequisite for obtaining accurate results.

You should generally normalize or scale the 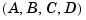matrices of a system to improve their conditioning. An example of a poorly scaled problem might be a dynamic system where two states in the state vector have units of light years and millimeters. You would expect the 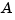matrix to contain both very large and very small numbers. Matrices containing numbers widely spread in value are often poorly conditioned both with respect to inversion and with respect to their eigenproblems, and inaccurate results can ensue.

Normalization also allows meaningful statements to be made about the degree of controllability and observability of the various inputs and outputs.

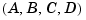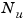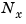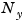A set of matrices can be normalized using diagonal scaling matrices , , and to scale u, x, and y.

so the normalized system is

where

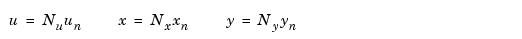
Choose the diagonal scaling matrices according to some appropriate normalization procedure. One criterion is to choose the maximum range of each of the input, state, and output variables. This method originated in the days of analog simulation computers when 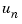, , 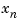and 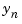were forced to be between 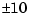Volts. A second method is to form scaling matrices where the diagonal entries are the smallest deviations that are significant to each variable. An excellent discussion of scaling is given in the introduction to the LINPACK Users' Guide, [1].

Choose scaling based upon physical insight to the problem at hand. If you choose not to scale, and for many small problems scaling is not necessary, be aware that this choice affects the accuracy of your answers.

Finally, note that the function ssbal performs automatic scaling of the state vector. Specifically, it seeks to minimize the norm of

by using diagonal scaling matrices 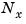. Such diagonal scaling is an economical way to compress the numerical range and improve the conditioning of subsequent state-space computations.

Zero-Pole-Gain Models

Summary