| Reliable Computations | |
Transfer Function
Transfer function models, when expressed in terms of expanded polynomials, tend to be inherently ill-conditioned representations of LTI systems. For systems of order greater than 10, or with very large/small polynomial coefficients, difficulties can be encountered with functions like roots, conv, bode, step, or conversion functions like ss or zpk.
A major difficulty is the extreme sensitivity of the roots of a polynomial to its coefficients. This example is adapted from Wilkinson, [6] as an illustration. Consider the transfer function
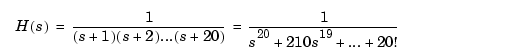
The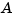 
matrix of the companion realization of 
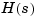is
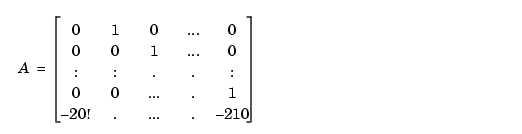
Despite the benign looking poles of the system (at -1,-2,..., -20) you are faced with a rather large range in the elements of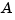 
, from 1 to 
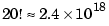. But the difficulties don't stop here. Suppose the coefficient of 
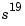in the transfer function (or 
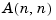) is perturbed from 210 to 
(
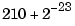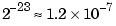). Then, computed on a VAX (IEEE arithmetic has enough mantissa for only 
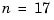), the poles of the perturbed transfer function (equivalently, the eigenvalues of 
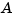) are
eig(A)' ans = Columns 1 through 7 -19.9998 -19.0019 -17.9916 -17.0217 -15.9594 -15.0516 -13.9504 Columns 8 through 14 -13.0369 -11.9805 -11.0081 -9.9976 -9.0005 -7.9999 -7.0000 Columns 15 through 20 -6.0000 -5.0000 -4.0000 -3.0000 -2.0000 -1.0000
The problem here is not roundoff. Rather, high-order polynomials are simply intrinsically very sensitive, even when the zeros are well separated. In this case, a relative perturbation of the order of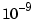 
induced relative perturbations of the order of 
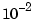in some roots. But some of the roots changed very little. This is true in general. Different roots have different sensitivities to different perturbations. Computed roots may then be quite meaningless for a polynomial, particularly high-order, with imprecisely known coefficients.
Finding all the roots of a polynomial (equivalently, the poles of a transfer function or the eigenvalues of a matrix in controllable or observable canonical form) is often an intrinsically sensitive problem. For a clear and detailed treatment of the subject, including the tricky numerical problem of deflation, consult [6].
It is therefore preferable to work with the factored form of polynomials when available. To compute a state-space model of the transfer function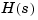 
defined above, for example, you could expand the denominator of 
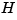, convert the transfer function model to state space, and extract the state-space data by
However, you should rather keep the denominator in factored form and work with the zero-pole-gain representation of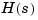 
.
Indeed, the resulting state matrix a2 is better conditioned.
and the conversion from zero-pole-gain to state space incurs no loss of accuracy in the poles.
format long e [sort(eig(a1)) sort(eig(a2))] ans = 9.999999999998792e-01 1.000000000000000e+00 2.000000000001984e+00 2.000000000000000e+00 3.000000000475623e+00 3.000000000000000e+00 3.999999981263996e+00 4.000000000000000e+00 5.000000270433721e+00 5.000000000000000e+00 5.999998194359617e+00 6.000000000000000e+00 7.000004542844700e+00 7.000000000000000e+00 8.000013753274901e+00 8.000000000000000e+00 8.999848908317270e+00 9.000000000000000e+00 1.000059459550623e+01 1.000000000000000e+01 1.099854678336595e+01 1.100000000000000e+01 1.200255822210095e+01 1.200000000000000e+01 1.299647702454549e+01 1.300000000000000e+01 1.400406940833612e+01 1.400000000000000e+01 1.499604787386921e+01 1.500000000000000e+01 1.600304396718421e+01 1.600000000000000e+01 1.699828695210055e+01 1.700000000000000e+01 1.800062935148728e+01 1.800000000000000e+01 1.899986934359322e+01 1.900000000000000e+01 2.000001082693916e+01 2.000000000000000e+01
There is another difficulty with transfer function models when realized in state-space form with ss. They may give rise to badly conditioned eigenvector matrices, even if the eigenvalues are well separated. For example, consider the normal matrix
Its eigenvectors and eigenvalues are given as follows.
[v,d] = eig(A) v = 0.7071 -0.0000 -0.3162 0.6325 -0.7071 0.0000 -0.3162 0.6325 0.0000 0.7071 0.6325 0.3162 -0.0000 -0.7071 0.6325 0.3162 d = 1.0000 0 0 0 0 2.0000 0 0 0 0 5.0000 0 0 0 0 10.0000
The condition number (with respect to inversion) of the eigenvector matrix is
Now convert a state-space model with the above A matrix to transfer function form, and back again to state-space form.
b = [1 ; 1 ; 0 ; -1]; c = [0 0 2 1]; H = tf(ss(A,b,c,0)); % transfer function [Ac,bc,cc] = ssdata(H) % convert back to state space
Note that Ac is not a standard companion matrix and has already been balanced as part of the ss conversion (see ssbal for details).
Note also that the eigenvectors have changed.
[vc,dc] = eig(Ac) vc = -0.5017 0.2353 0.0510 0.0109 -0.8026 0.7531 0.4077 0.1741 -0.3211 0.6025 0.8154 0.6963 -0.0321 0.1205 0.4077 0.6963 dc = 10.0000 0 0 0 0 5.0000 0 0 0 0 2.0000 0 0 0 0 1.0000
The condition number of the new eigenvector matrix
The phenomenon illustrated above is not unusual. Matrices in companion form or controllable/observable canonical form (like Ac) typically have worse-conditioned eigensystems than matrices in general state-space form (like A). This means that their eigenvalues and eigenvectors are more sensitive to perturbation. The problem generally gets far worse for higher-order systems. Working with high-order transfer function models and converting them back and forth to state space is numerically risky.
In summary, the main numerical problems to be aware of in dealing with transfer function models (and hence, calculations involving polynomials) are:
ss, while better than the standard companion form, often results in ill-conditioned eigenproblems, especially with higher-order systems.
The above statements hold even for systems with distinct poles, but are particularly relevant when poles are multiple.
| | State Space | Zero-Pole-Gain Models | |