Creating and Manipulating Models

Discretization of Systems with Delays

You can also use c2d to discretize SISO or MIMO continuous-time models with time delays. If Ts is the sampling period used for discretization:

• A delay of tau seconds in the continuous-time model is mapped to a delay of k sampling periods in the discretized model, where k = fix(tau/Ts).
• The residual fractional delay tau - k*Ts is absorbed into the coefficients of the discretized model (for the zero-order-hold and first-order-hold methods only).

For example, to discretize the transfer function

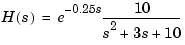
using zero-order hold on the input, and a 10 Hz sampling rate, type

• h = tf(10,[1 3 10],'inputdelay',0.25);
  hd = c2d(h,0.1)
  

This produces the discrete-time transfer function

• Transfer function:
           0.01187 z^2 + 0.06408 z + 0.009721
  z^(-2) * ----------------------------------
               z^3 - 1.655 z^2 + 0.7408 z
   
  Sampling time: 0.1
  

Here the input delay in 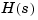amounts to 2.5 times the sampling period of 0.1 seconds. Accordingly, the discretized model hd inherits an input delay of two sampling periods, as confirmed by the value of hd.inputdelay. The residual half-period delay is factored into the coefficients of hd by the discretization algorithm.

The step responses of the continuous and discretized models are compared in the figure below. This plot was produced by the command

• step(h,'--',hd,'-')
  
  
  
  

Note    The Tustin and matched pole/zero methods are accurate only for delays that are integer multiples of the sampling period. It is therefore preferable to use the zoh and foh discretization methods for models with delays.

Matched Poles and Zeros

Resampling of Discrete-Time Models