

| MATLAB Function Reference |   |
Solve delay differential equations (DDEs) with constant delays
Syntax
sol = dde23(ddefun,lags,history,tspan) sol = dde23(ddefun,lags,history,tspan,options) sol = dde23(ddefun,lags,history,tspan,options,p1,p2,...)
Arguments
ddefun |
Function that evaluates the right side of the differential equations where |
lags |
Vector of constant, positive delays 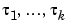 . . |
history |
Specify history in one of three ways: |
tspan |
Interval of integration as a vector [t0,tf] with t0 < tf. |
options |
Optional integration argument. A structure you create using the ddeset function. See ddeset for details. |
p1,p2,... |
Optional parameters that dde23 passes to ddefun, history if it is a function, and any functions you specify in options. |
Description
sol = dde23(ddefun,lags,history,tspan)
integrates the system of DDEs
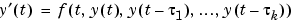
on the interval 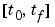 , where
, where 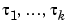 are constant, positive delays and
are constant, positive delays and 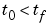 .
.
dde23 returns the solution as a structure sol. Use the auxiliary function deval and the output sol to evaluate the solution at specific points tint in the interval tspan = [t0,tf].
The structure sol returned by dde23 has the following fields.
sol.x |
Mesh selected by dde23 |
sol.y |
Approximation to 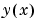 at the mesh points in at the mesh points in sol.x. |
sol.yp |
Approximation to 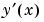 at the mesh points in at the mesh points in sol.x |
sol.solver |
Solver name, 'dde23' |
sol = dde23(ddefun,lags,history,tspan,options)
solves as above with default integration properties replaced by values in options, an argument created with ddeset. See ddeset and Initial Value Problems for DDEs in the MATLAB documentation for details.
Commonly used options are scalar relative error tolerance 'RelTol' (1e-3 by default) and vector of absolute error tolerances 'AbsTol' (all components are 1e-6 by default).
Use the 'Jumps' option to solve problems with discontinuities in the history or solution. Set this option to a vector that contains the locations of discontinuities in the solution prior to t0 (the history) or in coefficients of the equations at known values of 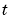 after
after t0.
Use the 'Events' option to specify a function that dde23 calls to find where functions
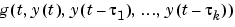 vanish. This function must be of the form
vanish. This function must be of the form
and contain an event function for each event to be tested. For the kth event function in events:
value(k) is the value of the kth event function.
isterminal(k) = 1 if you want the integration to terminate at a zero of this event function and 0 otherwise.
direction(k) = 0 if you want dde23 to compute all zeros of this event function, +1 if only zeros where the event function increases, and -1 if only zeros where the event function decreases.
If you specify the 'Events' option and events are detected, the output structure sol also includes fields:
sol = dde23(ddefun,lags,history,tspan,options,p1,p2,...)
passes the parameters p1,p2,... to the DDE function as ddefun(t,y,z,p1,p2,...), to the history function, if there is one, as history (t,p1,p2,...), and similarly to all functions specified in options. Use options = [] as a place holder if no options are set.
Examples
This example solves a DDE on the interval [0, 5] with lags 1 and 0.2. The function ddex1de computes the delay differential equations, and ddex1hist computes the history for t <= 0.
Note
The demo ddex1 contains the complete code for this example. To see the code in an editor, click the example name, or type edit ddex1 at the command line. To run the example type ddex1 at the command line.
|
This code evaluates the solution at 100 equally spaced points in the interval [0,5], then plots the result.
ddex1 shows how you can code this problem using subfunctions. For more examples see ddex2.
Algorithm
dde23 tracks discontinuities and integrates with the explicit Runge-Kutta (2,3) pair and interpolant of ode23. It uses iteration to take steps longer than the lags.
See Also
ddeget, ddeset, deval, @ (function_handle)
References
L.F. Shampine and S. Thompson, "Solving DDEs in MATLAB," Applied Numerical Mathematics, Vol. 37, 2001, pp. 441-458.
 | dbup | ddeadv |  |