ncx2cdf (Statistics Toolbox)

Noncentral chi-square cumulative distribution function (cdf)

Syntax

```
P = ncx2cdf(X,V,DELTA)
```

Description

P = ncx2cdf(X,V,DELTA) computes the noncentral chi-square cdf at each of the values in X using the corresponding degrees of freedom in V and positive noncentrality parameters in DELTA. Vector or matrix inputs for X, V, and DELTA must have the same size, which is also the size of P. A scalar input for X, V, or DELTA is expanded to a constant matrix with the same dimensions as the other inputs.

Some texts refer to this distribution as the generalized Rayleigh, Rayleigh-Rice, or Rice distribution.

The noncentral chi-square cdf is

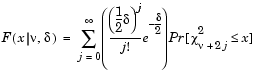
Example

x = (0:0.1:10)';
p1 = ncx2cdf(x,4,2);
p = chi2cdf(x,4);
plot(x,p,'--',x,p1,'-')

References

[1] Johnson, N., and S. Kotz, Distributions in Statistics: Continuous Univariate Distributions-2, John Wiley and Sons, 1970. pp. 130-148.

See Also
cdf, ncx2inv, ncx2pdf, ncx2rnd, ncx2stat

nctstat ncx2inv