Statistics Toolbox

Example: Generalized Linear Models

For example, consider the following data derived from the carbig data set. We have cars of various weights, and we record the total number of cars of each weight and the number qualifying as poor-mileage cars because their miles per gallon value is below some target. (Suppose we don't know the miles per gallon for each car, only the number passing the test.) It might be reasonable to assume that the value of the variable poor follows a binomial distribution with parameter N=total and with a p parameter that depends on the car weight. A plot shows that the proportion of poor-mileage cars follows a nonlinear S-shape.

• w = [2100 2300 2500 2700 2900 3100 3300 3500 3700 3900 4100 4300]';
  poor = [1 2 0 3 8 8 14 17 19 15 17 21]';
  total = [48 42 31 34 31 21 23 23 21 16 17 21]';
  [w poor total]
  ans =
          2100           1          48
          2300           2          42
          2500           0          31
          2700           3          34
          2900           8          31
          3100           8          21
          3300          14          23
          3500          17          23
          3700          19          21
          3900          15          16
          4100          17          17
          4300          21          21
  plot(w,poor./total,'x')
  
  
  

This shape is typical of graphs of proportions, as they have natural boundaries at 0.0 and 1.0.

A linear regression model would not produce a satisfactory fit to this graph. Not only would the fitted line not follow the data points, it would produce invalid proportions less than 0 for light cars, and higher than 1 for heavy cars.

There is a class of regression models for dealing with proportion data. The logistic model is one such model. It defines the relationship between proportion p and weight w to be

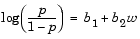
Is this a good model for our data? It would be helpful to graph the data on this scale, to see if the relationship appears linear. However, some of our proportions are 0 and 1, so we cannot explicitly evaluate the left-hand-side of the equation. A useful trick is to compute adjusted proportions by adding small increments to the poor and total values -- say a half observation to poor and a full observation to total. This keeps the proportions within range. A graph now shows a more nearly linear relationship.

• padj = (poor+.5) ./ (total+1);
  plot(w,log(padj./(1-padj)),'x')
  
  
  

We can use the glmfit function to fit this logistic model.

• b = glmfit(w,[poor total],'binomial')
  b =
    -13.3801
      0.0042
  

To use these coefficients to compute a fitted proportion, we have to invert the logistic relationship. Some simple algebra shows that the logistic equation can also be written as

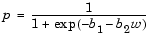
Fortunately, the function glmval can decode this link function to compute the fitted values. Using this function we can graph fitted proportions for a range of car weights, and superimpose this curve on the original scatter plot.

• x = 2100:100:4500;
  y = glmval(b,x,'logit');
  plot(w,poor./total,'x',x,y,'r-')
  
  
  

Generalized linear models can fit a variety of distributions with a variety of relationships between the distribution parameters and the predictors. A full description is beyond the scope of this document. For more information see Dobson (1990), or McCullagh and Nelder (1990). Also see the reference material for glmfit.

Generalized Linear Models

Robust and Nonparametric Methods