Statistics Toolbox

Fractional Factorial Designs

One difficulty with factorial designs is that the number of combinations increases exponentially with the number of variables you want to manipulate.

For example, the sensitivity study discussed above might be impractical if there were seven variables to study instead of just three. A full factorial design would require 2⁷ = 128 runs!

If we assume that the variables do not act synergistically in the system, we can assess the sensitivity with far fewer runs. The theoretical minimum number is eight. A design known as the Plackett-Burman design uses a Hadamard matrix to define this minimal number of runs. To see the design (X) matrix for the Plackett-Burman design, we use the hadamard function.

• X = hadamard(8)
  
  X =
       1     1     1     1     1     1     1     1
       1    -1     1    -1     1    -1     1    -1
       1     1    -1    -1     1     1    -1    -1
       1    -1    -1     1     1    -1    -1     1
       1     1     1     1    -1    -1    -1    -1
       1    -1     1    -1    -1     1    -1     1
       1     1    -1    -1    -1    -1     1     1
       1    -1    -1     1    -1     1     1    -1
  

The last seven columns are the actual variable settings (-1 for low, 1 for high.) The first column (all ones) allows us to measure the mean effect in the linear equation, .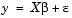

The Plackett-Burman design enables us to study the main (linear) effects of each variable with a small number of runs. It does this by using a fraction, in this case 8/128, of the runs required for a full factorial design. A drawback of this design is that if the effect of one variable does vary with the value of another variable, then the estimated effects will be biased (that is, they will tend to be off by a systematic amount).

At a cost of a somewhat larger design, we can find a fractional factorial that is much smaller than a full factorial, but that does allow estimation of main effects independent of interactions between pairs of variables. We can do this by specifying generators that control the confounding between variables.

As an example, suppose we create a design with the first four variables varying independently as in a full factorial, but with the other three variables formed by multiplying different triplets of the first four. With this design the effects of the last three variables are confounded with three-way interactions among the first four variables. The estimated effect of any single variable, however, is not confounded with (is independent of) interaction effects between any pair of variables. Interaction effects are confounded with each other. Box, Hunter, and Hunter [5] present the properties of these designs and provide the generators needed to produce them.

The fracfact function can produce this fractional factorial design using the generator strings that Box, Hunter, and Hunter provide.

• X = fracfact('a b c d abc bcd acd')
  X =
      -1    -1    -1    -1    -1    -1    -1
      -1    -1    -1     1    -1     1     1
      -1    -1     1    -1     1     1     1
      -1    -1     1     1     1    -1    -1
      -1     1    -1    -1     1     1    -1
      -1     1    -1     1     1    -1     1
      -1     1     1    -1    -1    -1     1
      -1     1     1     1    -1     1    -1
       1    -1    -1    -1     1    -1     1
       1    -1    -1     1     1     1    -1
       1    -1     1    -1    -1     1    -1
       1    -1     1     1    -1    -1     1
       1     1    -1    -1    -1     1     1
       1     1    -1     1    -1    -1    -1
       1     1     1    -1     1    -1    -1
       1     1     1     1     1     1     1
  

Full Factorial Designs

Response Surface Designs