| Statistics Toolbox | |
Empirical Cumulative Distribution Function
The ksdensity function described in the last section produces an empirical version of a probability density function (pdf). That is, instead of selecting a density with a particular parametric form and estimating the parameters, it produces a nonparametric density estimate that tries to adapt itself to the data.
Similarly, it is possible to produce an empirical version of the cumulative distribution function (cdf). The ecdf function computes this empirical cdf. It returns the values of a function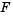 
such that 
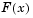represents the proportion of observations in a sample less than or equal to 
.
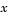The idea behind the empirical cdf is simple. It is a function that assigns probability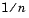 
to each of 
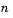observations in a sample. Its graph has a stair-step appearance. If a sample comes from a distribution in a parametric family (such as a normal distribution), its empirical cdf is likely to resemble the parametric distribution. If not, its empirical distribution still gives an estimate of the cdf for the distribution that generated the data.
In the following example, we generate 20 observations from a normal distribution with mean 10 and standard deviation 2. We use ecdf to calculate the empirical cdf and stairs to plot it. Then we overlay the normal distribution curve on the empirical function.
x = normrnd(10,2,20,1); [f,xf] = ecdf(x); stairs(xf,f) xx=linspace(5,15,100); yy = normcdf(xx,10,2); hold on; plot(xx,yy,'r:'); hold off legend('Empirical cdf','Normal cdf',2)
The empirical cdf is especially useful in survival analysis applications. In such applications the data may be censored, that is, not observed exactly. Some individuals may fail during a study, and we observe their failure time exactly. Other individuals may drop out of the study, or may not fail until after the study is complete. The ecdf function has arguments for dealing with censored data.
| | Probability Density Estimation | The Bootstrap | |
