Statistics Toolbox

canoncorr

Canonical correlation analysis

Syntax

• [A,B] = canoncorr(X,Y)
  [A,B,r] = canoncorr(X,Y)
  [A,B,r,U,V] = canoncorr(X,Y)
  [A,B,r,U,V,stats] = canoncorr(X,Y)
  

Description

[A,B] = canoncorr(X,Y) computes the sample canonical coefficients for the n-by-d1 and n-by-d2 data matrices X and Y. X and Y must have the same number of observations (rows) but can have different numbers of variables (columns). A and B are d1-by-d and d2-by-d matrices, where d = min(rank(X),rank(Y)). The jth columns of A and B contain the canonical coefficients, i.e., the linear combination of variables making up the jth canonical variable for X and Y, respectively. Columns of A and B are scaled to make the covariances of the canonical variables, or scores, the identity matrix (see U and V below). If X or Y is less than full rank, canoncorr gives a warning and returns zeros in the rows of A or B corresponding to dependent columns of X or Y.

[A,B,r] = canoncorr(X,Y) also returns a 1-by-d vector containing the sample canonical correlations. The jth element of r is the correlation between the jth columns of U and V (see below).

[A,B,r,U,V] = canoncorr(X,Y) also returns the canonical variables, known also as scores. U and V are n-by-d matrices computed as

• U = (X - repmat(mean(X),N,1))*A
  V = (Y - repmat(mean(Y),N,1))*B
  

[A,B,r,U,V,stats] = canoncorr(X,Y) also returns a structure containing information relating to the sequence of d null hypotheses 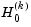, that the (k+1)st through dth correlations are all zero, for k = 0:(d-1). stats contains three fields, each a 1-by-d vector with elements corresponding to the values of k:

dfe	Error degrees of freedom, i.e., (d1-k)*(d2-k)
chisq	Bartlett's approximate chi-squared statistic for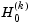
p	Right-tail significance level for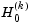

Examples

• load carbig;
  X = [Displacement Horsepower Weight Acceleration MPG];
  nans = sum(isnan(X),2) > 0;
  [A B r U V] = canoncorr(X(~nans,1:3), X(~nans,4:5));
  
  plot(U(:,1),V(:,1),'.');
  xlabel('0.0025*Disp + 0.020*HP - 0.000025*Wgt');
  ylabel('-0.17*Accel + -0.092*MPG')
  
  
  

See Also

manova1, princomp

References

[1]  Krzanowski, W.J., Principles of Multivariate Analysis, Oxford University Press, Oxford, 1988.

[2]  Seber, G.A.F., Multivariate Observations, Wiley, New York, 1984.

candgen

capable