Optimization Toolbox

Nonlinear Least-Squares with Full Jacobian Sparsity Pattern

The large-scale methods in lsqnonlin, lsqcurvefit, and fsolve can be used with small- to medium-scale problems without computing the Jacobian in fun or providing the Jacobian sparsity pattern. (This example also applies to the case of using fmincon or fminunc without computing the Hessian or supplying the Hessian sparsity pattern.) How small is small- to medium-scale? No absolute answer is available, as it depends on the amount of virtual memory available in your computer system configuration.

Suppose your problem has m equations and n unknowns. If the command J = sparse(ones(m,n)) causes an Out of memory error on your machine, then this is certainly too large a problem. If it does not result in an error, the problem might still be too large, but you can only find out by running it and seeing if MATLAB is able to run within the amount of virtual memory available on your system.

Let's say you have a small problem with 10 equations and 2 unknowns, such as finding x that minimizes

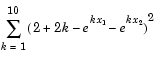
starting at the point x = [0.3, 0.4].

Because lsqnonlin assumes that the sum of squares is not explicitly formed in the user function, the function passed to lsqnonlin should instead compute the vector valued function

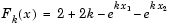
for 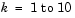(that is, F should have k components).

Step 1: Write an M-file myfun.m that computes the objective function values.

• function F = myfun(x)
  k = 1:10;
  F = 2 + 2*k-exp(k*x(1))-exp(k*x(2));
  

Step 2: Call the nonlinear least-squares routine.

• x0 = [0.3 0.4]            % Starting guess
  [x,resnorm] = lsqnonlin(@myfun,x0)     % Invoke optimizer
  

Because the Jacobian is not computed in myfun.m , and no Jacobian sparsity pattern is provided using the JacobPattern parameter in options, lsqnonlin calls the large-scale method with JacobPattern set to Jstr = sparse(ones(10,2)). This is the default for lsqnonlin. Note that the Jacobian parameter in options is 'off' by default.

When the finite-differencing routine is called the first time, it detects that Jstr is actually a dense matrix, i.e., that no speed benefit is derived from storing it as a sparse matrix. From then on the finite-differencing routine uses Jstr = ones(10,2) (a full matrix) for the optimization computations.

After about 24 function evaluations, this example gives the solution

• x = 
       0.2578   0.2578
  resnorm     % Residual or sum of squares
  resnorm = 
       124.3622
  

Most computer systems can handle much larger full problems, say into the 100's of equations and variables. But if there is some sparsity structure in the Jacobian (or Hessian) that can be taken advantage of, the large-scale methods will always run faster if this information is provided.

Nonlinear Equations with Jacobian Sparsity Pattern

Nonlinear Minimization with Gradient and Hessian