System Identification Toolbox

Some Special Topics

This section describes a number of miscellaneous topics. Most of the information here is also covered in other parts of the manual, but since manuals seldom are read from the beginning, you can also check if a particular topic is brought up here.

Time Series Modeling

When there is no input present, the general model (3-43) reduces to the ARMA model structure.

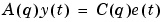
With 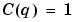you have an AR model structure.

Similarly, a state-space model for a time series is given by

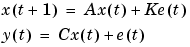
so that the matrices B and D are empty.

Basically all commands still apply to these time-series models, but with natural modifications. They are listed as follows.

• m= idpoly(A,[ ],C)
  e = iddata([],idinput(300,'rgs'))
  y = sim(m,e)
  

Spectral analysis (etfe and spa) returns results in the idfrd model format, that now just contains SpectrumData and its variance. bode will only plot these signal spectra and, if required, the confidence intervals.

• g = spa(y)
  p= etfe(y)
  bode(g,p,'sd',3)
  

Note that etfe gives the periodogram estimate p of the spectrum.

armax and arx work the same way, but need no specification of nb and nk.

• th = arx(y,na)
  th = armax(y,[na nc])
  

Note that arx also handles multivariable signals, and so do n4sid and pem.

• m = n4sid(y) %default order
  bode(m)
  compare(y,m,10) % 10-step ahead predictions being evaluated.
  

Structured state-space models of time series can be built simply by specifying B = [], D = [] in idss and idgrey. resid works the same way for time series models, but does not provide any input-residual correlation plots.

• resid(m,y)
  

In addition there are two commands that are specifically constructed for building scalar AR models of time series. One is

• m = ar(y,na)
  

which has an option that allows you to choose the algorithm from a group of several popular techniques for computing the least squares AR model. Among these are Burg's method, a geometric lattice method, the Yule-Walker approach, and a modified covariance method. See Function Reference for details. The other command is

• m = ivar(y,na)
  

which uses an instrumental variables technique to compute the AR part of a time series.

Finally, when no input is present, the functions bj, iv, iv4, and oe are not of interest.

Here is an example where you can simulate a time series, compare spectral estimates and covariance function estimates, and also the predictions of the model.

• ts0 = idpoly([1 -1.5 0.7],[]);
  ir = sim(ts0,[1;zeros(24,1)]);
  Ry0 = conv(ir,ir(25:-1:1)); % The true covariance function
  e = idinput(200,'rgs');
  y = sim(ts0,e);
  plot(y)
  per = etfe(y);
  speh = spa(y);
  ffplot(per,speh,ts0)
  ts2 = ar(y,2); % A second order AR model:
  ffplot(speh,ts2,ts0,'sd',3)
  % The covariance function estimates:
  Ryh = covf(y,25);
  Ryh = [Ryh(end:-1:2),Ryh]';
  ir2 = sim(ts2,[1;zeros(24,1)]);
  Ry2 = conv(ir2,ir2(25:-1:1));
  plot([-24:24]'*ones(1,3),[Ryh,Ry2,Ry0])
  % The prediction ability of the model:
  compare(y,ts2,5)
  

Segmentation of Data

Periodic Inputs