

| Financial Toolbox |   |
Dividing Matrices
Matrix division is useful primarily for solving equations, and especially for solving simultaneous linear equations (see the next section). For example, you want to solve for X in A*X = B.
In ordinary algebra, you would simply divide both sides of the equation by A, and X would equal B/A. However, since matrix algebra is not commutative (A*X 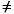 X*A), different processes apply. In formal matrix algebra, the solution involves matrix inversion. MATLAB, however, simplifies the process by providing two matrix division symbols, left and right (
X*A), different processes apply. In formal matrix algebra, the solution involves matrix inversion. MATLAB, however, simplifies the process by providing two matrix division symbols, left and right (\ and /). In general,
X = A\B solves for X in A*X = B
X = B/A solves for X in X*A = B.
In general, matrix A must be a nonsingular square matrix; i.e., it must be invertible and it must have the same number of rows and columns. (Generally, a matrix is invertible if the matrix times its inverse equals the identity matrix. To understand the theory and proofs, please consult a textbook on linear algebra such as the one by Hill listed in the "Bibliography.") MATLAB gives a warning message if the matrix is singular or nearly so.
 | Multiplying Matrices | Solving Simultaneous Linear Equations |  |