Function Reference

zpk

Specify zero-pole-gain models or convert LTI model to zero-pole-gain form

Syntax

• sys = zpk(z,p,k)
  sys = zpk(z,p,k,Ts)
  sys = zpk(M)
  sys = zpk(z,p,k,ltisys)
  
  sys = zpk(z,p,k,'Property1',Value1,...,'PropertyN',ValueN)
  sys = zpk(z,p,k,Ts,'Property1',Value1,...,'PropertyN',ValueN)
  
  sys = zpk('s')
  sys = zpk('z')
  
  zsys = zpk(sys)
  zsys = zpk(sys,'inv')    % for state-space sys only
  

Description

zpk is used to create zero-pole-gain models (ZPK objects) or to convert TF or SS models to zero-pole-gain form.

Creation of Zero-Pole-Gain Models

sys = zpk(z,p,k) creates a continuous-time zero-pole-gain model with zeros z, poles p, and gain(s) k. The output sys is a ZPK object storing the model data (see "LTI Objects" on page 2-3).

In the SISO case, z and p are the vectors of real- or complex-valued zeros and poles, and k is the real- or complex-valued scalar gain.

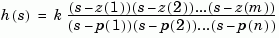
Set z or p to [] for systems without zeros or poles. These two vectors need not have equal length and the model need not be proper (that is, have an excess of poles).

You can also use rational expressions to create a ZPK model. To do so, use either:

• s = zpk('s') to specify a ZPK model from a rational transfer function of the Laplace variable, s.
• z = zpk('z',Ts) to specify a ZPK model with sample time Ts from a rational transfer function of the discrete-time variable, z.

Once you specify either of these variables, you can specify ZPK models directly as real- or complex-valued rational expressions in the variable s or z.

To create a MIMO zero-pole-gain model, specify the zeros, poles, and gain of each SISO entry of this model. In this case:

• z and p are cell arrays of vectors with as many rows as outputs and as many columns as inputs, and k is a matrix with as many rows as outputs and as many columns as inputs.
• The vectors z{i,j} and p{i,j} specify the zeros and poles of the transfer function from input j to output i.
• k(i,j) specifies the (scalar) gain of the transfer function from input j to output i.

See below for a MIMO example.

sys = zpk(z,p,k,Ts) creates a discrete-time zero-pole-gain model with sample time Ts (in seconds). Set Ts = -1 or Ts = [] to leave the sample time unspecified. The input arguments z, p, k are as in the continuous-time case.

sys = zpk(M) specifies a static gain M.

sys = zpk(z,p,k,ltisys) creates a zero-pole-gain model with generic LTI properties inherited from the LTI model ltisys (including the sample time). See "Generic Properties" on page 2-26 for an overview of generic LTI properties.

To create an array of ZPK models, use a for loop, or use multidimensional cell arrays for z and p, and a multidimensional array for k.

Any of the previous syntaxes can be followed by property name/property value pairs.

• 'PropertyName',PropertyValue
  

Each pair specifies a particular LTI property of the model, for example, the input names or the input delay time. See set entry and the example below for details. Note that

• sys = zpk(z,p,k,'Property1',Value1,...,'PropertyN',ValueN)
  

is a shortcut for the following sequence of commands.

• sys = zpk(z,p,k)
  set(sys,'Property1',Value1,...,'PropertyN',ValueN)
  

Zero-Pole-Gain Models as Rational Expressions in s or z

You can also use rational expressions to create a ZPK model. To do so, first type either:

• s = zpk('s') to specify a ZPK model using a rational function in the Laplace variable, s.
• z = zpk('z',Ts) to specify a ZPK model with sample time Ts using a rational function in the discrete-time variable, z.

Once you specify either of these variables, you can specify ZPK models directly as rational expressions in the variable s or z by entering your transfer function as a rational expression in either s or z.

Conversion to Zero-Pole-Gain Form

zsys = zpk(sys) converts an arbitrary LTI model sys to zero-pole-gain form. The output zsys is a ZPK object. By default, zpk uses zero to compute the zeros when converting from state-space to zero-pole-gain. Alternatively,

• zsys = zpk(sys,'inv')
  

uses inversion formulas for state-space models to compute the zeros. This algorithm is faster but less accurate for high-order models with low gain at .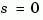

Variable Selection

As for transfer functions, you can specify which variable to use in the display of zero-pole-gain models. Available choices include 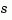(default) and 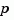for continuous-time models, and 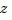(default), 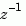, or 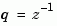for discrete-time models. Reassign the 'Variable' property to override the defaults. Changing the variable affects only the display of zero-pole-gain models.

Example

Example 1

Specify the following zero-pole-gain model.

To do this, type

• z = {[] ; -0.5}
  p = {0.3 ; [0.1+i 0.1-i]}
  k = [1 ; 2]
  H = zpk(z,p,k,-1)    % unspecified sample time
  

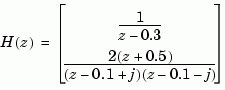
Example 2

Convert the transfer function

• h = tf([-10 20 0],[1 7 20 28 19 5])
  Transfer function:
               -10 s^2 + 20 s
  ----------------------------------------
  s^5 + 7 s^4 + 20 s^3 + 28 s^2 + 19 s + 5
  

to zero-pole-gain form by typing

• zpk(h)
  Zero/pole/gain:
       -10 s (s-2)
  ----------------------
  (s+1)^3 (s^2 + 4s + 5)
  

Example 3

Create a discrete-time ZPK model from a rational expression in the variable z, by typing

• z = zpk('z',0.1); 
  H = (z+.1)*(z+.2)/(z^2+.6*z+.09)
  Zero/pole/gain:
  (z+0.1) (z+0.2)
  ---------------
     (z+0.3)^2
   
  Sampling time: 0.1
  

Algorithm

zpk uses the MATLAB function roots to convert transfer functions and the functions zero and pole to convert state-space models.

See Also
frd         Convert to frequency response data models

get         Get properties of LTI models

set         Set properties of LTI models

ss          Convert to state-space models

tf          Convert to TF transfer function models

zpkdata     Retrieve zero-pole-gain data

zgrid

zpkdata