

| Function Reference |   |
Syntax
Description
norm
computes the 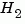 or
or 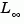 norm of a continuous- or discrete-time LTI model.
norm of a continuous- or discrete-time LTI model.
H2 Norm
The 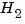 norm of a stable continuous system with transfer function
norm of a stable continuous system with transfer function 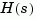 , is the root-mean-square of its impulse response, or equivalently
, is the root-mean-square of its impulse response, or equivalently

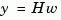 to unit white noise inputs
to unit white noise inputs 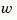 .
.

Infinity Norm
The infinity norm is the peak gain of the frequency response, that is,
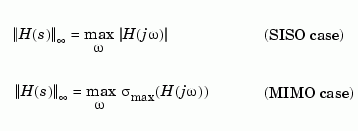
where 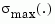 denotes the largest singular value of a matrix.
denotes the largest singular value of a matrix.
The discrete-time counterpart is
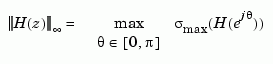
Usage
norm(sys) or norm(sys,2) both return the 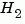 norm of the TF, SS, or ZPK model
norm of the TF, SS, or ZPK model sys. This norm is infinite in the following cases:
sys is unstable.
sys is continuous and has a nonzero feedthrough (that is, nonzero gain at the frequency 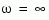 ).
).
Note that norm(sys) produces the same result as
norm(sys,inf) computes the infinity norm of any type of LTI model sys. This norm is infinite if sys has poles on the imaginary axis in continuous time, or on the unit circle in discrete time.
norm(sys,inf,tol) sets the desired relative accuracy on the computed infinity norm (the default value is tol=1e-2).
[ninf,fpeak] = norm(sys,inf) also returns the frequency fpeak where the gain achieves its peak value.
Example
Consider the discrete-time transfer function
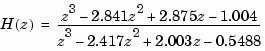
with sample time 0.1 second. Compute its 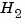 norm by typing
norm by typing
Compute its infinity norm by typing
These values are confirmed by the Bode plot of 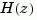 .
.
The gain indeed peaks at approximately 3 rad/sec and its peak value in dB is found by typing
Algorithm
norm uses the same algorithm as covar for the 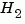 norm, and the algorithm of [1] for the infinity norm.
norm, and the algorithm of [1] for the infinity norm. sys is first converted to state space.
See Also
bode
freqresp
sigma
References
[1] Bruisma, N.A. and M. Steinbuch, "A Fast Algorithm to Compute the 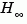 -Norm of a Transfer Function Matrix," System Control Letters, 14 (1990), pp. 287-293.
-Norm of a Transfer Function Matrix," System Control Letters, 14 (1990), pp. 287-293.
 | nichols | nyquist |  |