Creating and Manipulating Models

Frequency Response Data (FRD) Models

In some instances, you may only have sampled frequency response data, rather than a transfer function or state-space model for the system you want to analyze or control. For information on frequency response analysis of linear systems, see Chapter 8 of [1].

For example, suppose the frequency response function for the SISO system you want to model is G(w). Suppose, in addition, that you perform an experiment to evaluate G(w) at a fixed set of frequencies, 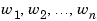. You can do this by driving the system with a sequence of sinusoids at each of these frequencies, as depicted below.

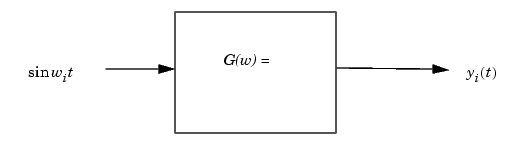
Here 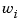is the input frequency of each sinusoid, i = 1 ... n, and G(w) = 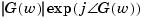. The steady state output response of this system satisfies

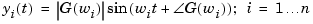
A frequency response data (FRD) object is a model form you can use to store frequency response data (complex frequency response, along with a corresponding vector of frequency points) that you obtain either through simulations or experimentally. In this example, the frequency response data is obtained from the set of response pairs:

.

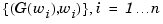Once you store your data in an FRD model, you can treat it as an LTI model, and manipulate an FRD model in most of the same ways you manipulate TF, SS, and ZPK models.

The basic syntax for creating a SISO FRD model is

• sys = frd(response,frequencies,units)
  

where

• frequencies is a real vector of length Nf.
• response is a vector of length Nf of complex frequency response values for these frequencies.
• units is an optional string for the units of frequency: either 'rad/s' (default) or 'Hz'

For example, the MAT-file LTIexamples.mat contains a frequency vector freq, and a corresponding complex frequency response data vector respG. To load this frequency-domain data and construct an FRD model, type

• load LTIexamples
  sys = frd(respG,freq)
  Continuous-time frequency response with 1 output and 1 input
  at 5 frequency points.
  From input 1 to: 
  Frequency(rad/s)        output 1     
  ----------------        --------     
          1         -0.812505 -0.000312i
          2         -0.092593 -0.462963i
          4         -0.075781 -0.001625i
          5         -0.043735 -0.000390i
  

The syntax for creating a MIMO FRD model is the same as for the SISO case, except that response is a p-by-m-by-Nf multidimensional array, where p is the number of outputs, m is the number of inputs, and Nf is the number of frequency data points (the length of frequency).

The following table summarizes the complex-valued response data format for FRD models.

Table 1-3: Data Format for the Argument response in FRD Models 

Model Form		Response Data Format
SISO model		Vector of length Nf for which response(i) is the frequency response at the frequency frequency(i)
MIMO model with Ny outputs and Nu inputs		Ny-by-Nu-by-Nf multidimensional array for which response(i,j,k) specifies the frequency response from input j to output i at frequency frequency(k)
S1-by-...-by-Sn array of models with Ny outputs and Nu inputs		Ny-by-Nu-by-S1-by-...-by-Sn multidimensional array, for which response(i,j,k,:) specifies the array of frequency response data from input j to output i at frequency frequency(k)

Descriptor State-Space Models

Discrete-Time Models