LTI Models (Creating and Manipulating Models)

Creating and Manipulating Models

Zero-Pole-Gain Models

This section explains how to specify continuous-time SISO and MIMO zero-pole-gain models. The specification for discrete-time zero-pole-gain models is a simple extension of the continuous-time case. See Discrete-Time Models.

SISO Zero-Pole-Gain Models

Continuous-time SISO zero-pole-gain models are of the form

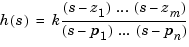
where 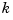is a real-valued scalar (the gain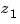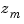), and ,..., and 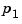,..., 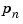are the real or complex conjugate pairs of zeros and poles of the transfer function 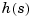. This model is closely related to the transfer function representation: the zeros are simply the numerator roots, and the poles, the denominator roots.

There are two ways to specify SISO zero-pole-gain models:

Using the zpk command

As rational expressions in the Laplace variable s

The syntax to specify ZPK models directly using zpk is

```
h = zpk(z,p,k)
```

where z and p are the vectors of zeros and poles, and k is the gain. This produces a ZPK object h that encapsulates the z, p, and k data. For example, typing

```
h = zpk(0, [1-i 1+i 2], -2)
```

produces

Zero/pole/gain:
         -2 s
--------------------
(s-2) (s^2 - 2s + 2)

You can also specify zero-pole-gain models as rational expressions in the Laplace variable s by:

Defining the variable s as a ZPK model
- ```
s = zpk('s')
```
Entering the transfer function as a rational expression in s.

For example, once s is defined with zpk,

```
H = -2s/((s - 2)*(s^2 + 2*s + 2));
```

returns the same ZPK model as

```
h = zpk([0], [2 -1-i -1+i ], -2);
```

Note You need only define the ZPK variable s once. All subsequent rational expressions of s will be ZPK models, unless you convert the variable s to TF. See Model Conversion for more information on conversion to other model types.

MIMO Zero-Pole-Gain Models

Just as with TF models, you can also specify a MIMO ZPK model by concatenation of its SISO entries (see Model Interconnection Functions).

You can also use the command zpk to specify MIMO ZPK models. The syntax to create a p-by-m MIMO zero-pole-gain model using zpk is

```
H = zpk(Z,P,K)
```

where

Z is the p-by-m cell array of zeros (Z{i,j} = zeros of )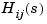

P is the p-by-m cell array of poles (P{i,j} = poles of )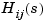

K is the p-by-m matrix of gains (K(i,j) = gain of )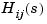

For example, typing

Z = {[],-5;[1-i 1+i] []};    
P = {0,[-1 -1];[1 2 3],[]};
K = [-1  3;2  0];
H = zpk(Z,P,K)

creates the two-input/two-output zero-pole-gain model

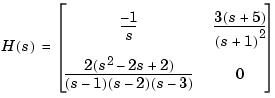
Notice that you use [] as a place-holder in Z (or P) when the corresponding entry of 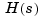has no zeros (or poles).

Transfer Function Models State-Space Models