Wavelet Toolbox

intwave

Integrate wavelet function psi

Syntax

• [INTEG,XVAL] = intwave('wname',PREC)
  [INTEG,XVAL] = intwave('wname',PREC,PFLAG)
  [INTEG,XVAL] = intwave('wname')
  

Description

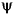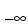[INTEG,XVAL] = intwave('wname',PREC) computes the integral, INTEG, of the wavelet function (from to XVAL values):

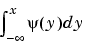for x in XVAL.

The function 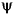is approximated on the 2PREC points grid XVAL where PREC is a positive integer. 'wname' is a string containing the name of the wavelet 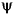(see wfilters for more information).

Output argument INTEG is a real or complex vector depending on the wavelet type.

For biorthogonal wavelets,

[INTDEC,XVAL,INTREC] = intwave('wname',PREC) computes the integrals, INTDEC and INTREC, of the wavelet decomposition function 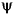_dec and the wavelet reconstruction function 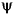_rec.

[INTEG,XVAL] = intwave('wname',PREC) is equivalent to [INTEG,XVAL] = intwave('wname',PREC,0).

[INTEG,XVAL] = intwave('wname') is equivalent to [INTEG,XVAL] = intwave('wname',8).

When used with three arguments intwave('wname',IN2,IN3), PREC = max(IN2,IN3) and plots are given.

When IN2 is equal to the special value 0, intwave('wname',0) is equivalent to intwave('wname',8,IN3).

intwave('wname') is equivalent to intwave('wname',8).

intwave is used only for continuous analysis (see cwt for more information).

Examples

• % Set wavelet name. 
  wname = 'db4';
  
  % Plot wavelet function. 
  [phi,psi,xval] = wavefun(wname,7);
  subplot(211); plot(xval,psi); title('Wavelet'); 
  
  % Compute and plot wavelet integrals approximations 
  % on a dyadic grid. 
  [integ,xval] = intwave(wname,7); 
  subplot(212); plot(xval,integ); 
  title(['Wavelet integrals over [-Inf x] ' ... 
         'for each value of xval']);
  
  
  

Algorithm

First, the wavelet function is approximated on a grid of 2^PREC points using wavefun. A piecewise constant interpolation is used to compute the integrals using cumsum.

See Also
wavefun

ind2depo

isnode