Wavelet Toolbox

Algorithms

• Given a signal s of length N, the DWT consists of log₂N stages at most. Starting from s, the first step produces two sets of coefficients: approximation coefficients cA₁, and detail coefficients cD₁. These vectors are obtained by convolving s with the low-pass filter Lo_D for approximation, and with the high-pass filter Hi_D for detail, followed by dyadic decimation.

More precisely, the first step is

The length of each filter is equal to 2N. If n = length (s), the signals F and G are of length n + 2N - 1, and then the coefficients cA₁ and cD₁ are of length

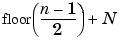
The next step splits the approximation coefficients cA₁ in two parts using the same scheme, replacing s by cA₁ and producing cA₂ and cD₂, and so on.

So the wavelet decomposition of the signal s analyzed at level j has the following structure: [cA_j, cD_j, ..., cD₁].

This structure contains for J = 3 the terminal nodes of the following tree.

• Conversely, starting from cA_j and cD_j, the IDWT reconstructs cA_j-1, inverting the decomposition step by inserting zeros and convolving the results with the reconstruction filters.

  

• For images, a similar algorithm is possible for two-dimensional wavelets and scaling functions obtained from one-dimensional wavelets by tensorial product.

• This kind of two-dimensional DWT leads to a decomposition of approximation coefficients at level j in four components: the approximation at level j + 1 and the details in three orientations (horizontal, vertical, and diagonal).

  The following charts describe the basic decomposition and reconstruction steps for images.

  

  

So, for J = 2, the two-dimensional wavelet tree has the following form.

Finally, let us mention that, for biorthogonal wavelets, the same algorithms hold but the decomposition filters on one hand and the reconstruction filters on the other hand are obtained from two distinct scaling functions associated with two multiresolution analyses in duality.

In this case, the filters for decomposition and reconstruction are, in general, of different odd lengths. This situation occurs, for example, for "splines" biorthogonal wavelets used in the toolbox. By zero-padding, the four filters can be extended in such a way that they will have the same even length.

Filters Used to Calculate the DWT and IDWT

Why Does Such an Algorithm Exist?