Statistics Toolbox

Hypergeometric Distribution

The following sections provide an overview of the hypergeometric distribution.

Background of the Hypergeometric Distribution

The hypergeometric distribution models the total number of successes in a fixed size sample drawn without replacement from a finite population.

The distribution is discrete, existing only for nonnegative integers less than the number of samples or the number of possible successes, whichever is greater. The hypergeometric distribution differs from the binomial only in that the population is finite and the sampling from the population is without replacement.

The hypergeometric distribution has three parameters that have direct physical interpretations. M is the size of the population. K is the number of items with the desired characteristic in the population. n is the number of samples drawn. Sampling "without replacement" means that once a particular sample is chosen, it is removed from the relevant population for all subsequent selections.

Definition of the Hypergeometric Distribution

The hypergeometric pdf is

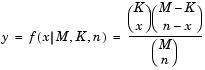
Example and Plot of the Hypergeometric Distribution

The plot shows the cdf of an experiment taking 20 samples from a group of 1000 where there are 50 items of the desired type.

• x = 0:10;
  y = hygecdf(x,1000,50,20);
  stairs(x,y)
  
  
  

Geometric Distribution

Lognormal Distribution