Statistics Toolbox

Two-Way Analysis of Variance (ANOVA)

The purpose of two-way ANOVA is to find out whether data from several groups have a common mean. One-way ANOVA and two-way ANOVA differ in that the groups in two-way ANOVA have two categories of defining characteristics instead of one.

Suppose an automobile company has two factories, and each factory makes the same three models of car. It is reasonable to ask if the gas mileage in the cars varies from factory to factory as well as from model to model. We use two predictors, factory and model, to explain differences in mileage.

There could be an overall difference in mileage due to a difference in the production methods between factories. There is probably a difference in the mileage of the different models (irrespective of the factory) due to differences in design specifications. These effects are called additive.

Finally, a factory might make high mileage cars in one model (perhaps because of a superior production line), but not be different from the other factory for other models. This effect is called an interaction. It is impossible to detect an interaction unless there are duplicate observations for some combination of factory and car model.

Two-way ANOVA is a special case of the linear model. The two-way ANOVA form of the model is

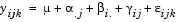
where, with respect to the automobile example above:

• y_ijk is a matrix of gas mileage observations (with row index i, column index j, and repetition index k).
• µ is a constant matrix of the overall mean gas mileage.
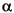• _.j is a matrix whose columns are the deviations of each car's gas mileage (from the mean gas mileage µ) that are attributable to the car's model. All values in a given column of 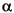_.j are identical, and the values in each row of 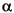_.j sum to 0.
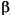• _i. is a matrix whose rows are the deviations of each car's gas mileage (from the mean gas mileage µ) that are attributable to the car's factory. All values in a given row of 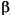_i. are identical, and the values in each column of 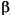_i. sum to 0.
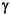• _ij is a matrix of interactions. The values in each row of 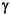_ij sum to 0, and the values in each column of 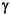_ij sum to 0.
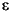• _ijk is a matrix of random disturbances.

The next section provides an example of a two-way analysis.

Example: Multiple Comparisons

Example: Two-Way ANOVA