Statistics Toolbox

D-Optimal Designs

The designs above pre-date the computer age, and some were in use by early in the 20th century. In the 1970s statisticians started to use the computer in experimental design by recasting the design of experiments (DOE) in terms of optimization. A D-optimal design is one that maximizes the determinant of Fisher's information matrix, X^TX. This matrix is proportional to the inverse of the covariance matrix of the parameters. So maximizing det(X^TX) is equivalent to minimizing the determinant of the covariance of the parameters.

A D-optimal design minimizes the volume of the confidence ellipsoid of the regression estimates of the linear model parameters, .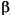

There are several functions in the Statistics Toolbox that generate D-optimal designs. These are cordexch, daugment, dcovary, and rowexch. The following sections explore D-optimal design in greater detail:

• Generating D-Optimal Designs
• Augmenting D-Optimal Designs
• Designing Experiments with Uncontrolled Inputs
• Controlling Candidate Points
• Including Categorical Factors

Box-Behnken Designs

Generating D-Optimal Designs