betapdf (Statistics Toolbox)

Beta probability density function (pdf)

Syntax

```
Y = betapdf(X,A,B)
```

Description

Y = betapdf(X,A,B) computes the beta pdf at each of the values in X using the corresponding parameters in A and B. Vector or matrix inputs for X, A, and B must all have the same size. A scalar input is expanded to a constant matrix with the same dimensions of the other inputs. The parameters in A and B must all be positive, and the values in X must lie on the interval [0 1].

The beta probability density function for a given value x and given pair of parameters a and b is

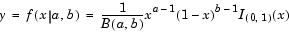
where B( · ) is the Beta function. The result, y, is the probability that a single observation from a beta distribution with parameters a and b will have value x. The indicator function 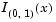ensures that only values of x in the range (0 1) have nonzero probability. The uniform distribution on (0 1) is a degenerate case of the beta pdf where a = 1 and b = 1.

A likelihood function is the pdf viewed as a function of the parameters. Maximum likelihood estimators (MLEs) are the values of the parameters that maximize the likelihood function for a fixed value of x.

Examples

a = [0.5 1; 2 4]
a =
    0.5000    1.0000
    2.0000    4.0000
y = betapdf(0.5,a,a)
y =
    0.6366    1.0000
    1.5000    2.1875

betalike betarnd