

| Function Reference |   |
Specify state-space models or convert an LTI model to state space
Syntax
sys = ss(a,b,c,d) sys = ss(a,b,c,d,Ts) sys = ss(d) sys = ss(a,b,c,d,ltisys) sys = ss(a,b,c,d,'Property1',Value1,...,'PropertyN',ValueN) sys = ss(a,b,c,d,Ts,'Property1',Value1,...,'PropertyN',ValueN) sys_ss = ss(sys) sys_ss = ss(sys,'minimal')
Description
ss
is used to create real- or complex-valued state-space models (SS objects) or to convert transfer function or zero-pole-gain models to state space.
Creation of State-Space Models
sys = ss(a,b,c,d)
creates the continuous-time state-space model
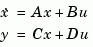
For a model with Nx states, Ny outputs, and Nu inputs:
a is an Nx-by-Nx real- or complex-valued matrix.
b is an Nx-by-Nu real- or complex-valued matrix.
c is an Ny-by-Nx real- or complex-valued matrix.
d is an Ny-by-Nu real- or complex-valued matrix.
The output sys is an SS model that stores the model data (see "State-Space Models" on page 2-14). If 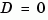 , you can simply set
, you can simply set d to the scalar 0 (zero), regardless of the dimension.
sys = ss(a,b,c,d,Ts)
creates the discrete-time model
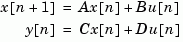
with sample time Ts (in seconds). Set Ts = -1 or Ts = [] to leave the sample time unspecified.
sys = ss(d)
specifies a static gain matrix 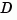 and is equivalent to
and is equivalent to
sys = ss(a,b,c,d,ltisys)
creates a state-space model with generic LTI properties inherited from the LTI model ltisys (including the sample time). See "Generic Properties" on page 2-26 for an overview of generic LTI properties.
See "Building LTI Arrays" on page 4-12 for information on how to build arrays of state-space models.
Any of the previous syntaxes can be followed by property name/property value pairs.
Each pair specifies a particular LTI property of the model, for example, the input names or some notes on the model history. See the set entry and the example below for details. Note that
is equivalent to the sequence of commands.
Conversion to State Space
sys_ss = ss(sys)
converts an arbitrary TF or ZPK model sys to state space. The output sys_ss is an equivalent state-space model (SS object). This operation is known as state-space realization.
sys_ss = ss(sys,'minimal') produces a state-space realization with no uncontrollable or unobservable states. This is equivalent to sys_ss = minreal(ss(sys)).
Example 1
sys = ss(A,B,C,D,0.05,'statename',{'position' 'velocity'},... 'inputname','force',... 'notes','Created 10/15/96')
creates a discrete-time model with matrices 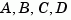 and sample time 0.05 second. This model has two states labeled
and sample time 0.05 second. This model has two states labeled position and velocity, and one input labeled force (the dimensions of 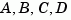 should be consistent with these numbers of states and inputs). Finally, a note is attached with the date of creation of the model.
should be consistent with these numbers of states and inputs). Finally, a note is attached with the date of creation of the model.
Example 2
Compute a state-space realization of the transfer function
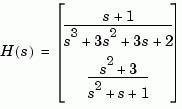
H = [tf([1 1],[1 3 3 2]) ; tf([1 0 3],[1 1 1])]; sys = ss(H); size(sys) State-space model with 2 outputs, 1 input, and 5 states.
Note that the number of states is equal to the cumulative order of the SISO entries of H(s).
To obtain a minimal realization of H(s), type
The resulting state-space model order has order three, the minimum number of states needed to represent H(s). This can be seen directly by factoring H(s) as the product of a first order system with a second order one.
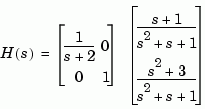
See Also
dss Specify descriptor state-space models.
frd Specify FRD models or convert to an FRD.
get Get properties of LTI models.
set Set properties of LTI models.
ssdata Retrieve the 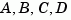 matrices of state-space model.
matrices of state-space model.
tf Specify transfer functions or convert to TF.
zpk Specify zero-pole-gain models or convert to ZPK.
 | sminreal | ss2ss |  |