Function Reference

obsvf

Compute the observability staircase form

Syntax

• [Abar,Bbar,Cbar,T,k] = obsvf(A,B,C)
  [Abar,Bbar,Cbar,T,k] = obsvf(A,B,C,tol)
  

Description

If the observability matrix of (A,C) has rank 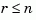, where n is the size of A, then there exists a similarity transformation such that

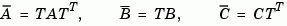
where 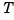is unitary and the transformed system has a staircase form with the unobservable modes, if any, in the upper left corner.

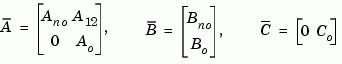
where 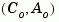is observable, and the eigenvalues of 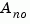are the unobservable modes.

[Abar,Bbar,Cbar,T,k] = obsvf(A,B,C) decomposes the state-space system with matrices A, B, and C into the observability staircase form Abar, Bbar, and Cbar, as described above. T is the similarity transformation matrix and k is a vector of length n, where n is the number of states in A. Each entry of k represents the number of observable states factored out during each step of the transformation matrix calculation [1]. The number of nonzero elements in k indicates how many iterations were necessary to calculate T, and sum(k) is the number of states in 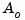, the observable portion of Abar.

obsvf(A,B,C,tol) uses the tolerance tol when calculating the observable/unobservable subspaces. When the tolerance is not specified, it defaults to 10*n*norm(a,1)*eps.

Example

Form the observability staircase form of

• A =
       1     1
       4    -2
  
  B =
       1    -1
       1    -1
  
  C =
       1     0
       0     1
  

by typing

• [Abar,Bbar,Cbar,T,k] = obsvf(A,B,C)
  Abar =
       1     1
       4    -2
  Bbar =
       1     1
       1    -1
  Cbar =
       1     0
       0     1
  T =
       1     0
       0     1
  k =
       2     0
  

Algorithm

obsvf is an M-file that implements the Staircase Algorithm of [1] by calling ctrbf and using duality.

See Also
ctrbf       Compute the controllability staircase form

obsv        Calculate the observability matrix

             References

[1] Rosenbrock, M.M., State-Space and Multivariable Theory, John Wiley, 1970.

obsv

ord2