modred (Function Reference)

Model order reduction

Syntax

rsys = modred(sys,elim)
rsys = modred(sys,elim,'mdc')
rsys = modred(sys,elim,'del')

Description

modred reduces the order of a continuous or discrete state-space model sys. This function is usually used in conjunction with balreal. Two order reduction techniques are available:

rsys = modred(sys,elim) or rsys = modred(sys,elim,'mdc') produces a reduced-order model rsys with matching DC gain (or equivalently, matching steady state in the step response). The index vector elim specifies the states to be eliminated. The resulting model rsys has length(elim) fewer states. This technique consists of setting the derivative of the eliminated states to zero and solving for the remaining states.
rsys = modred(sys,elim,'del')simply deletes the states specified by elim. While this method does not guarantee matching DC gains, it tends to produce better approximations in the frequency domain (see example below).

If the state-space model sys has been balanced with balreal and the grammians have 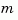small diagonal entries, you can reduce the model order by eliminating the last 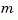states with modred.

Example

Consider the continuous fourth-order model

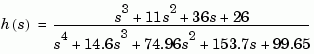
To reduce its order, first compute a balanced state-space realization with balreal by typing

h = tf([1 11 36 26],[1 14.6 74.96 153.7 99.65])
[hb,g] = balreal(h)
g'

MATLAB returns

ans =
   1.3938e-01   9.5482e-03   6.2712e-04   7.3245e-06

The last three diagonal entries of the balanced grammians are small, so eliminate the last three states with modred using both matched DC gain and direct deletion methods.

hmdc = modred(hb,2:4,'mdc')
hdel = modred(hb,2:4,'del')

Both hmdc and hdel are first-order models. Compare their Bode responses against that of the original model .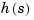

```
bode(h,'-',hmdc,'x',hdel,'*')
```

The reduced-order model hdel is clearly a better frequency-domain approximation of 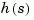. Now compare the step responses.

```
step(h,'-',hmdc,'-.',hdel,'--')
```

While hdel accurately reflects the transient behavior, only hmdc gives the true steady-state response.

Algorithm

The algorithm for the matched DC gain method is as follows. For continuous-time models

the state vector is partitioned into 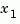, to be kept, and 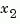, to be eliminated.

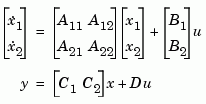
Next, the derivative of 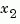is set to zero and the resulting equation is solved for 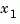. The reduced-order model is given by

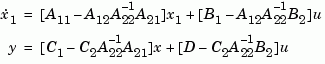
The discrete-time case is treated similarly by setting

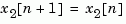
Limitations

With the matched DC gain method, 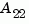must be invertible in continuous time, and 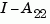must be invertible in discrete time.

See Also
balreal Input/output balancing of state-space models

minreal Minimal state-space realizations

minreal ndims