

| Function Reference |   |
Solve continuous-time Lyapunov equations
Syntax
Description
lyap
solves the special and general forms of the Lyapunov matrix equation. Lyapunov equations arise in several areas of control, including stability theory and the study of the RMS behavior of systems.
X = lyap(A,Q)
solves the Lyapunov equation
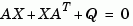
where 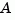 and
and 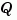 are square matrices of identical sizes. The solution
are square matrices of identical sizes. The solution X is a symmetric matrix if 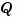 is.
is.
X = lyap(A,B,C)
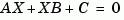
The matrices 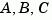 must have compatible dimensions but need not be square.
must have compatible dimensions but need not be square.
Algorithm
lyap transforms the 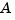 and
and 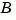 matrices to complex Schur form, computes the solution of the resulting triangular system, and transforms this solution back [1].
matrices to complex Schur form, computes the solution of the resulting triangular system, and transforms this solution back [1].
Limitations
The continuous Lyapunov equation has a (unique) solution if the eigenvalues 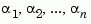 of
of 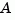 and
and 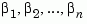 of
of 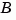 satisfy
satisfy
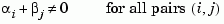
If this condition is violated, lyap produces the error message
See Also
covar Covariance of system response to white noise
dlyap Solve discrete Lyapunov equations
References
[1] Bartels, R.H. and G.W. Stewart, "Solution of the Matrix Equation AX + XB = C," Comm. of the ACM, Vol. 15, No. 9, 1972.
[2] Bryson, A.E. and Y.C. Ho, Applied Optimal Control, Hemisphere Publishing, 1975. pp. 328-338.
 | ltiview | margin |  |