

| Function Reference |   |
Convert discrete-time LTI models to continuous time
Syntax
Description
d2c converts LTI models from discrete to continuous time using one of the following conversion methods:
The string method specifies the conversion method. If method is omitted then zero-order hold ('zoh') is assumed. See "Continuous/Discrete Conversions of LTI Models" for more details on the conversion methods.
Example
Consider the discrete-time model with transfer function
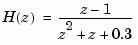
and sample time 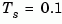 second. You can derive a continuous-time zero-order-hold equivalent model by typing
second. You can derive a continuous-time zero-order-hold equivalent model by typing
Discretizing the resulting model Hc with the zero-order hold method (this is the default method) and sampling period 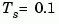 gives back the original discrete model
gives back the original discrete model 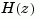 . To see this, type
. To see this, type
To use the Tustin approximation instead of zero-order hold, type
As with zero-order hold, the inverse discretization operation
Algorithm
The 'zoh' conversion is performed in state space and relies on the matrix logarithm (see logm in the MATLAB documentation).
Limitations
The Tustin approximation is not defined for systems with poles at 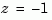 and is ill-conditioned for systems with poles near
and is ill-conditioned for systems with poles near 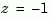 .
.
The zero-order hold method cannot handle systems with poles at 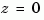 . In addition, the
. In addition, the 'zoh' conversion increases the model order for systems with negative real poles, [2]. This is necessary because the matrix logarithm maps real negative poles to complex poles. As a result, a discrete model with a single pole at 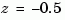 would be transformed to a continuous model with a single complex pole at
would be transformed to a continuous model with a single complex pole at
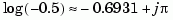 . Such a model is not meaningful because of its complex time response.
. Such a model is not meaningful because of its complex time response.
To ensure that all complex poles of the continuous model come in conjugate pairs, d2c replaces negative real poles 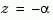 with a pair of complex conjugate poles near
with a pair of complex conjugate poles near 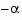 . The conversion then yields a continuous model with higher order. For example, the discrete model with transfer function
. The conversion then yields a continuous model with higher order. For example, the discrete model with transfer function
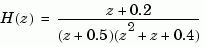
and sample time 0.1 second is converted by typing
Warning: System order was increased to handle real negative poles. Zero/pole/gain: -33.6556 (s-6.273) (s^2 + 28.29s + 1041) -------------------------------------------- (s^2 + 9.163s + 637.3) (s^2 + 13.86s + 1035)
Convert Hc back to discrete time by typing
Zero/pole/gain: (z+0.5) (z+0.2) ------------------------- (z+0.5)^2 (z^2 + z + 0.4) Sampling time: 0.1
This discrete model coincides with 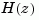 after canceling the pole/zero pair at
after canceling the pole/zero pair at 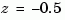 .
.
See Also
c2d Continuous- to discrete-time conversion
d2d Resampling of discrete models
logm Matrix logarithm
References
[1] Franklin, G.F., J.D. Powell, and M.L. Workman, Digital Control of Dynamic Systems, Second Edition, Addison-Wesley, 1990.
[2] Kollár, I., G.F. Franklin, and R. Pintelon, "On the Equivalence of z-domain and s-domain Models in System Identification," Proceedings of the IEEE Instrumentation and Measurement Technology Conference, Brussels, Belgium, June, 1996, Vol. 1, pp. 14-19.
 | ctrbf | d2d |  |