Creating and Manipulating Models

Transfer Function Models

This section explains how to specify continuous-time SISO and MIMO transfer function models. The specification of discrete-time transfer function models is a simple extension of the continuous-time case (see Discrete-Time Models). In this section you can also read about how to specify transfer functions consisting of pure gains.

SISO Transfer Function Models

A continuous-time SISO transfer function

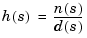
is characterized by its numerator 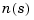and denominator 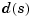, both polynomials of the Laplace variable s.

There are two ways to specify SISO transfer functions:

• Using the tf command
• As rational expressions in the Laplace variable s

To specify a SISO transfer function model 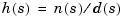using the tf command, type

• h = tf(num,den)
  

where num and den are row vectors listing the coefficients of the polynomials 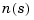and 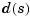, respectively, when these polynomials are ordered in descending powers of s. The resulting variable h is a TF object containing the numerator and denominator data.

For example, you can create the transfer function

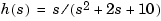by typing

• h = tf([1 0],[1 2 10])
  

MATLAB responds with

• Transfer function:
         s
  --------------
  s^2 + 2 s + 10
  

Note the customized display used for TF objects.

You can also specify transfer functions as rational expressions in the Laplace variable s by:

1. Defining the variable s as a special TF model

   • s = tf('s');
     

2. Entering your transfer function as a rational expression in s

For example, once s is defined with tf as in 1,

• H = s/(s^2 + 2*s +10);
  

produces the same transfer function as

• h = tf([1 0],[1 2 10]);
  

Note    You need only define the variable s as a TF model once. All of the subsequent models you create using rational expressions of s are specified as TF objects, unless you convert the variable s to ZPK. See "Model Conversion" on page 1-39 for more information.

MIMO Transfer Function Models

MIMO transfer functions are two-dimensional arrays of elementary SISO transfer functions. There are several ways to specify MIMO transfer function models, including:

• Concatenation of SISO transfer function models
• Using tf with cell array arguments

Consider the rational transfer matrix

.

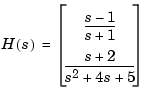
You can specify 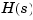by concatenation of its SISO entries. For instance,

• h11 = tf([1 -1],[1 1]);
  h21 = tf([1 2],[1 4 5]);
  

or, equivalently,

• s = tf('s')
  h11 = (s-1)/(s+1);
  h21 = (s+2)/(s^2+4*s+5); 
  

can be concatenated to form .

• H = [h11; h21]
  

This syntax mimics standard matrix concatenation and tends to be easier and more readable for MIMO systems with many inputs and/or outputs. See Model Interconnection Functions for more details on concatenation operations for LTI systems.

Alternatively, to define MIMO transfer functions using tf, you need two cell arrays (say, N and D) to represent the sets of numerator and denominator polynomials, respectively. See Structures and Cell Arrays in the MATLAB documentation for more details on cell arrays.

For example, for the rational transfer matrix 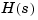, the two cell arrays N and D should contain the row-vector representations of the polynomial entries of

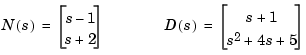
You can specify this MIMO transfer matrix 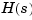by typing

• N = {[1 -1];[1 2]}; % cell array for N(s)
  D = {[1 1];[1 4 5]}; % cell array for D(s)
  H = tf(N,D)
  

MATLAB responds with

• Transfer function from input to output...
        s - 1
   #1:  -----
        s + 1
   
            s + 2
   #2:  -------------
        s^2 + 4 s + 5
  

Notice that both N and D have the same dimensions as H. For a general MIMO transfer matrix 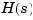, the cell array entries N{i,j} and D{i,j} should be row-vector representations of the numerator and denominator of 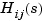, the 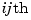entry of the transfer matrix .

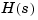Pure Gains

You can use tf with only one argument to specify simple gains or gain matrices as TF objects. For example,

• G = tf([1 0;2 1])
  

produces the gain matrix

while

• E = tf
  

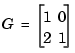
creates an empty transfer function.

Creating LTI Models

Zero-Pole-Gain Models