Creating and Manipulating Models

Zero-Order Hold

Zero-order hold (ZOH) devices convert sampled signals to continuous-time signals for analyzing sampled continuous-time systems. The zero-order-hold discretization 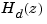of a continuous-time LTI model 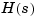is depicted in the following block diagram.

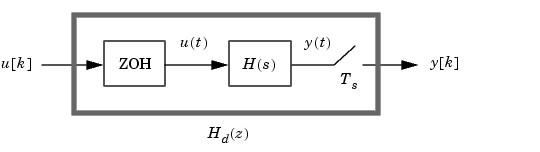
The ZOH device generates a continuous input signal u(t) by holding each sample value u[k] constant over one sample period.

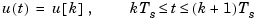
The signal 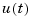is then fed to the continuous system 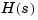, and the resulting output 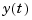is sampled every 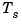seconds to produce .

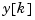Conversely, given a discrete system 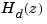, the d2c conversion produces a continuous system 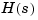whose ZOH discretization coincides with 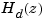. This inverse operation has the following limitations:

• d2c cannot operate on LTI models with poles at 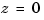when the ZOH is used.
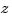• Negative real poles in the domain are mapped to pairs of complex poles in the 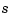domain. As a result, the d2c conversion of a discrete system with negative real poles produces a continuous system with higher order.

The next example illustrates the behavior of d2c with real negative poles. Consider the following discrete-time ZPK model.

• hd = zpk([],-0.5,1,0.1)
  Zero/pole/gain:
     1
  -------
  (z+0.5)
   
  Sampling time: 0.1
  

Use d2c to convert this model to continuous-time

• hc = d2c(hd)     
  

and you get a second-order model.

• Zero/pole/gain:
     4.621 (s+149.3)
  ---------------------
  (s^2 + 13.86s + 1035)
  

Discretize the model again

• c2d(hc,0.1)      
  

and you get back the original discrete-time system (up to canceling the pole/zero pair at z=-0.5):

• Zero/pole/gain:
   (z+0.5)
  ---------
  (z+0.5)^2
   
  Sampling time: 0.1
  

Continuous/Discrete Conversions of LTI Models

First-Order Hold