Getting Started

Example: LQG Design

As an example of LQG design, consider the regulation problem illustrated below.

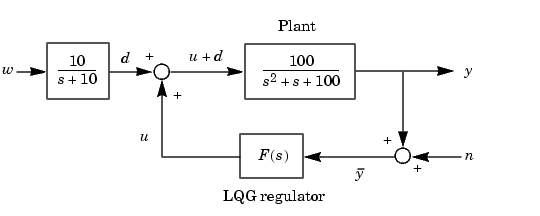
Figure 4-51: Simple Regulation Loop

The goal is to regulate the plant output 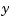around zero. The input disturbance 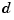is low frequency with power spectral density (PSD) concentrated below 10 rad/sec. For LQG design purposes, it is modeled as white noise driving a low-pass filter with a cutoff at 10 rad/sec, as this figure shows.

This figure shows the Bode magnitude of the shaping filter.

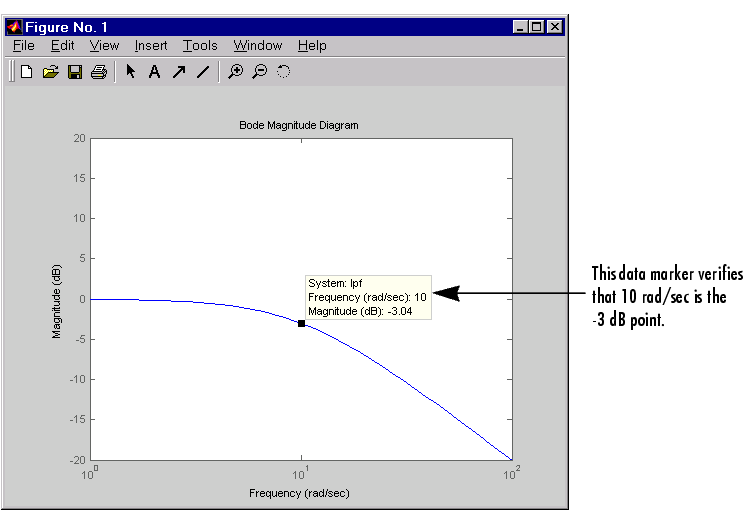
Figure 4-52: Bode Magnitude of the Low-Pass Filter

There is some measurement noise 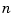, with noise intensity given by

Use the cost function

to specify the trade-off between regulation performance and cost of control. Note that an open-loop state-space model is

where 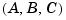is a state-space realization of .

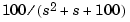The following commands design the optimal LQG regulator 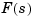for this problem.

• sys = ss(tf(100,[1 1 100])) % State-space plant model
  
  % Design LQ-optimal gain K
  K = lqry(sys,10,1) % u = -Kx minimizes J(u)
  
  % Separate control input u and disturbance input d
  P = sys(:,[1 1]);
  % input [u;d], output y
  
  % Design Kalman state estimator Kest.
  Kest = kalman(P,1,0.01)
  
  % Form LQG regulator = LQ gain + Kalman filter.
  F = lqgreg(Kest,K)
  

The last command returns a state-space model F of the LQG regulator 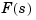. Note that lqry, kalman, and lqgreg perform discrete-time LQG design when applied to discrete plants.

To validate the design, close the loop with feedback, create and add the lowpass filter in series with the closed-loop system, and compare the open- and closed-loop impulse responses by using the impulse function.

• % Close loop
  clsys = feedback(sys,F,+1)    % Note positive feedback.
  
  % Create the lowpass filter and add it in series with clsys.
  s = tf('s');
  lpf= 10/(s+10) ;
  clsys_fin = lpf*clsys;
  
  % Open- vs. closed-loop impulse responses
  impulse(sys,'r--',clsys_fin,'b-')
  

This figure compares the open- and closed-loop impulse responses for this example.

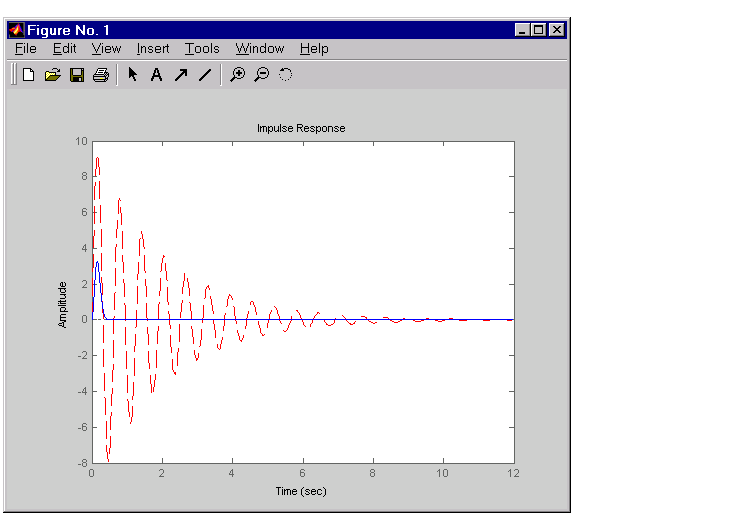
Figure 4-53: Comparison of Open- and Closed-Loop Impulse Response for the LQG Example

Linear-Quadratic-Gaussian (LQG) Design

Example: LQG Design for Set Point Tracking