Statistics Toolbox

Noncentral Chi-Square Distribution

The following sections provide an overview of the noncentral 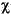² distribution.

Background of the Noncentral Chi-Square Distribution

The 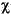² distribution is actually a simple special case of the noncentral chi-square distribution. One way to generate random numbers with a 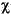² distribution (with 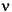degrees of freedom) is to sum the squares of 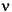standard normal random numbers (mean equal to zero.)

What if we allow the normally distributed quantities to have a mean other than zero? The sum of squares of these numbers yields the noncentral chi-square distribution. The noncentral chi-square distribution requires two parameters; the degrees of freedom and the noncentrality parameter. The noncentrality parameter is the sum of the squared means of the normally distributed quantities.

The noncentral chi-square has scientific application in thermodynamics and signal processing. The literature in these areas may refer to it as the Ricean or generalized Rayleigh distribution.

Definition of the Noncentral Chi-Square Distribution

There are many equivalent formulas for the noncentral chi-square distribution function. One formulation uses a modified Bessel function of the first kind. Another uses the generalized Laguerre polynomials. The Statistics Toolbox computes the cumulative distribution function values using a weighted sum of 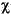² probabilities with the weights equal to the probabilities of a Poisson distribution. The Poisson parameter is one-half of the noncentrality parameter of the noncentral chi-square.

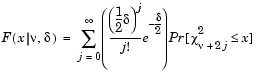
where 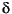is the noncentrality parameter.

Example of the Noncentral Chi-Square Distribution

The following commands generate a plot of the noncentral chi-square pdf.

• x = (0:0.1:10)';
  p1 = ncx2pdf(x,4,2);
  p = chi2pdf(x,4);
  plot(x,p,'--',x,p1,'-')
  
  
  

Chi-Square Distribution

Discrete Uniform Distribution