Statistics Toolbox

Mathematical Foundations of Multiple Linear Regression

The linear model takes its common form

where:

• y is an n-by-1 vector of observations.
• X is an n-by-p matrix of regressors.
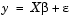
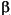• is a p-by-1 vector of parameters.
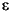• is an n-by-1 vector of random disturbances.

The solution to the problem is a vector, b, which estimates the unknown vector of parameters, 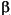. The least squares solution is

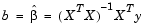
This equation is useful for developing later statistical formulas, but has poor numeric properties. regress uses QR decomposition of X followed by the backslash operator to compute b. The QR decomposition is not necessary for computing b, but the matrix R is useful for computing confidence intervals.

You can plug b back into the model formula to get the predicted y values at the data points.

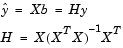
Statisticians use a hat (circumflex) over a letter to denote an estimate of a parameter or a prediction from a model. The projection matrix H is called the hat matrix, because it puts the "hat" on y.

The residuals are the difference between the observed and predicted y values.

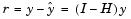
The residuals are useful for detecting failures in the model assumptions, since they correspond to the errors, 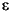, in the model equation. By assumption, these errors each have independent normal distributions with mean zero and a constant variance.

The residuals, however, are correlated and have variances that depend on the locations of the data points. It is a common practice to scale ("Studentize") the residuals so they all have the same variance.

In the equation below, the scaled residual, t_i, has a Student's t distribution with (n-p-1) degrees of freedom

where

and:

• t_i is the scaled residual for the ith data point.
• r_i is the raw residual for the ith data point.
• n is the sample size.
• p is the number of parameters in the model.
• h_i is the ith diagonal element of H.

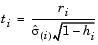
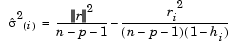
The left-hand side of the second equation is the estimate of the variance of the errors excluding the ith data point from the calculation.

A hypothesis test for outliers involves comparing t_i with the critical values of the t distribution. If t_i is large, this casts doubt on the assumption that this residual has the same variance as the others.

A confidence interval for the mean of each error is

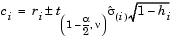
Confidence intervals that do not include zero are equivalent to rejecting the hypothesis (at a significance probability of 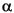) that the residual mean is zero. Such confidence intervals are good evidence that the observation is an outlier for the given model.

Multiple Linear Regression

Example: Multiple Linear Regression