| Statistics Toolbox |
  |
Hypothesis Test Terminology
To get started, there are some terms to define and assumptions to make:
- The null hypothesis is the original assertion. In this case the null hypothesis is that the average price of a gallon of gas is $1.15. The notation is H0: µ = 1.15.
- There are three possibilities for the alternative hypothesis. You might only be interested in the result if gas prices were actually higher. In this case, the alternative hypothesis is H1: µ > 1.15. The other possibilities are H1: µ < 1.15 and H1: µ
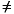 1.15.
1.15.
- The significance level is related to the degree of certainty you require in order to reject the null hypothesis in favor of the alternative. By taking a small sample you cannot be certain about your conclusion. So you decide in advance to reject the null hypothesis if the probability of observing your sampled result is less than the significance level. For a typical significance level of 5%, the notation is
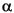 = 0.05. For this significance level, the probability of incorrectly rejecting the null hypothesis when it is actually true is 5%. If you need more protection from this error, then choose a lower value of
= 0.05. For this significance level, the probability of incorrectly rejecting the null hypothesis when it is actually true is 5%. If you need more protection from this error, then choose a lower value of 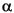 .
.
- The p-value is the probability of observing the given sample result under the assumption that the null hypothesis is true. If the p-value is less than
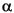 , then you reject the null hypothesis. For example, if
, then you reject the null hypothesis. For example, if 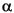 = 0.05 and the p-value is 0.03, then you reject the null hypothesis.
= 0.05 and the p-value is 0.03, then you reject the null hypothesis.
- The converse is not true. If the p-value is greater than
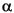 , you have insufficient evidence to reject the null hypothesis.
, you have insufficient evidence to reject the null hypothesis.
- The outputs for many hypothesis test functions also include confidence intervals. Loosely speaking, a confidence interval is a range of values that have a chosen probability of containing the true hypothesized quantity. Suppose, in our example, 1.15 is inside a 95% confidence interval for the mean, µ. That is equivalent to being unable to reject the null hypothesis at a significance level of 0.05. Conversely if the 100(1-
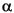 ) confidence interval does not contain 1.15, then you reject the null hypothesis at the
) confidence interval does not contain 1.15, then you reject the null hypothesis at the 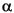 level of significance.
level of significance.
 | Hypothesis Tests | | Hypothesis Test Assumptions |  |




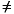 1.15.
1.15.
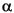 = 0.05. For this significance level, the probability of incorrectly rejecting the null hypothesis when it is actually true is 5%. If you need more protection from this error, then choose a lower value of
= 0.05. For this significance level, the probability of incorrectly rejecting the null hypothesis when it is actually true is 5%. If you need more protection from this error, then choose a lower value of 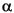 .
.
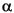 , then you reject the null hypothesis. For example, if
, then you reject the null hypothesis. For example, if 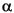 = 0.05 and the p-value is 0.03, then you reject the null hypothesis.
= 0.05 and the p-value is 0.03, then you reject the null hypothesis.
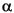 , you have insufficient evidence to reject the null hypothesis.
, you have insufficient evidence to reject the null hypothesis.
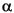 ) confidence interval does not contain 1.15, then you reject the null hypothesis at the
) confidence interval does not contain 1.15, then you reject the null hypothesis at the 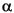 level of significance.
level of significance.

