

| Signal Processing Toolbox |   |
Compute the average filter delay (group delay)
Syntax
[gd,w]=grpdelay(b,a,l) [gd,f]=grpdelay(b,a,l,fs) [gd,w]=grpdelay(b,a,l,'whole') [gd,f]=grpdelay(b,a,l,'whole',fs) gd=grpdelay(b,a,w) gd=grpdelay(b,a,f,fs) grpdelay(b,a) grpdelay(Hd)
Description
The group delay of a filter is a measure of the average delay of the filter as a function of frequency. It is the negative first derivative of the phase response of the filter. If the complex frequency response of a filter is 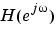 , then the group delay is
, then the group delay is
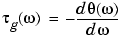
where 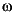 is frequency and
is frequency and 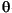 is the phase angle of
is the phase angle of 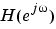 .
.
[gd,w] returns the = grpdelay(b,a,l)
i-point group delay, 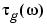 , of the digital filter
, of the digital filter
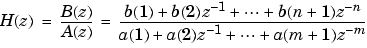
given the numerator and denominator coefficients in vectors b and a. grpdelay returns both gd, the group delay, and w, a vector containing the l frequency points in radians. grpdelay evaluates the group delay at l points equally spaced around the upper half of the unit circle, so w contains l points between 0 and 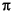 .
.
[gd,f] specifies a positive sampling frequency = grpdelay(b,a,l,fs)
fs in hertz. It returns a length l vector f containing the actual frequency points at which the group delay is calculated, also in hertz. f contains l points between 0 and fs/2.
[gd,w] and = grpdelay(b,a,l,'whole')
[gd,f] use = grpdelay(b,a,l,'whole',fs)
n points around the whole unit circle (from 0 to 2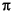 , or from 0 to
, or from 0 to fs).
gd return the group delay evaluated at the points in = grpdelay(b,a,f,fs)
w (in radians) or f (in hertz), respectively, where fs is the sampling frequency in hertz.
grpdelay(b,a)
with no output arguments plots the group delay versus frequency in the current figure window.
grpdelay(Hd)
plots the group delay and displays the plot in fvtool. The input Hd is a dfilt filter object.
grpdelay works for both real and complex input systems.
Examples
Plot the group delay of Butterworth filter b(z)/a(z):
The same example using a dfilt object and displaying the result in the Filter Visualization Tool (fvtool) is
Plot both the group and phase delays of a system on the same graph:
gd=grpdelay(b,a,512); gd(1)=[]; % Avoid NaNs [h,w]=freqz(b,a,512); h(1)=[]; w(1)=[]; pd=-unwrap(angle(h))./w; plot(w,gd,w,pd,':') xlabel('Frequency (rad/sec)'); grid; legend('Group Delay','Phase Delay');
Algorithm
grpdelay multiplies the filter coefficients by a unit ramp. After Fourier transformation, this process corresponds to differentiation.
See Also
cceps, fft, freqz, hilbert, icceps, rceps
 | goertzel | hamming |  |