

| Optimization Toolbox |   |
Typical Problems and How to Deal with Them
Optimization problems can take many iterations to converge and can be sensitive to numerical problems such as truncation and round-off error in the calculation of finite-difference gradients. Most optimization problems benefit from good starting guesses. This improves the execution efficiency and can help locate the global minimum instead of a local minimum.
Advanced problems are best solved by an evolutionary approach, whereby a problem with a smaller number of independent variables is solved first. You can generally use solutions from lower order problems as starting points for higher order problems by using an appropriate mapping.
The use of simpler cost functions and less stringent termination criteria in the early stages of an optimization problem can also reduce computation time. Such an approach often produces superior results by avoiding local minima.
The Optimization Toolbox functions can be applied to a large variety of problems. Used with a little "conventional wisdom," you can overcome many of the limitations associated with optimization techniques. Additionally, you can handle problems that are not typically in the standard form by using an appropriate transformation. Below is a list of typical problems and recommendations for dealing with them.
| Problem |
Recommendation |
| There is no guarantee that you have a global minimum unless your problem is continuous and has only one minimum. Starting the optimization from a number of different starting points can help to locate the global minimum or verify that there is only one minimum. Use different methods, where possible, to verify results. |
|
fminunc produces warning messages and seems to exhibit slow convergence near the solution. |
If you are not supplying analytically determined gradients and the termination criteria are stringent, fminunc often exhibits slow convergence near the solution due to truncation error in the gradient calculation. Relaxing the termination criteria produces faster, although less accurate, solutions. For the medium-scale algorithm, another option is adjusting the finite-difference perturbation levels, DiffMinChange and DiffMaxChange, which might increase the accuracy of gradient calculations. |
Sometimes an optimization problem has values of x for which it is impossible to evaluate the objective function fun or the nonlinear constraints function nonlcon. |
Place bounds on the independent variables or make a penalty function to give a large positive value to f and g when infeasibility is encountered. For gradient calculation, the penalty function should be smooth and continuous. |
| The function that is being minimized has discontinuities. |
The derivation of the underlying method is based upon functions with continuous first and second derivatives. Some success might be achieved for some classes of discontinuities when they do not occur near solution points. One option is to smooth the function. For example, the objective function might include a call to an interpolation function to do the smoothing. Or, for the medium-scale algorithms, you can adjust the finite-difference parameters in order to jump over small discontinuities. The variables DiffMinChange and DiffMaxChange control the perturbation levels for x used in the calculation of finite-difference gradients. The perturbation, 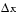 , is always in the range , is always in the range DiffMinChange < Dx < DiffMaxChange. |
| Warning messages are displayed. |
This sometimes occurs when termination criteria are overly stringent, or when the problem is particularly sensitive to changes in the independent variables. This usually indicates truncation or round-off errors in the finite-difference gradient calculation, or problems in the polynomial interpolation routines. These warnings can usually be ignored because the routines continue to make steps toward the solution point; however, they are often an indication that convergence will take longer than normal. Scaling can sometimes improve the sensitivity of a problem. |
The independent variables, 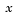 , can only take on discrete values, for example, integers. , can only take on discrete values, for example, integers. |
This type of problem commonly occurs when, for example, the variables are the coefficients of a filter that are realized using finite-precision arithmetic or when the independent variables represent materials that are manufactured only in standard amounts. Although the Optimization Toolbox functions are not explicitly set up to solve discrete problems, you can solve some discrete problems by first solving an equivalent continuous problem. Do this by progressively eliminating discrete variables from the independent variables, which are free to vary. Eliminate a discrete variable by rounding it up or down to the nearest best discrete value. After eliminating a discrete variable, solve a reduced order problem for the remaining free variables. Having found the solution to the reduced order problem, eliminate another discrete variable and repeat the cycle until all the discrete variables have been eliminated. dfildemo is a demonstration routine that shows how filters with fixed-precision coefficients can be designed using this technique. |
| The minimization routine appears to enter an infinite loop or returns a solution that does not satisfy the problem constraints. |
Your objective (fun), constraint (nonlcon, seminfcon), or gradient (computed by fun) functions might be returning Inf, NaN, or complex values. The minimization routines expect only real numbers to be returned. Any other values can cause unexpected results. Insert some checking code into the user-supplied functions to verify that only real numbers are returned (use the function isfinite). |
You do not get the convergence you expect from the lsqnonlin routine. |
You might be forming the sum of squares explicitly and returning a scalar value. lsqnonlin expects a vector (or matrix) of function values that are squared and summed internally. |
 | Optimization of Inline Objects Instead of M-Files | Converting Your Code to Version 2 Syntax |  |