

| System Identification Toolbox |   |
Residual Analysis
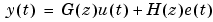
the noise source e(t) represents that part of the output that the model could not reproduce. It gives the "left-overs" or, in Latin, the residuals. For a good model, the residuals should be independent of the input. Otherwise, there would be more in the output that originates from the input and that the model has not picked up.
To test this independence, the cross-correlation function between input and residuals is computed by checking the Model View Model Residuals. It is wise to also display the confidence region for this function. For an ideal model the correlation function should lie entirely between the confidence lines for positive lags. If, for example, there is a peak outside the confidence region for lag k, this means that there is something in the output y(t) that originates from u(t-k) and that has not been properly described by the model. The test is carried out using the Validation Data. If these were not used to estimate the model, the test is quite tough. See also Model Structure Selection and Validation.
For a model also to give a correct description of the disturbance properties (i.e., the transfer function H), the residuals should be mutually independent. This test is also carried out by the view Model Residuals, by displaying the auto-correlation function of the residuals (excluding lag zero, for which this function by definition is 1). For an ideal model, the correlation function should be entirely inside the confidence region.
 | Compare Measured and Model Output | Text Information |  |