

| System Identification Toolbox |   |
Estimate the parameters of an AR model for scalar time series.
Syntax
Description
The parameters of the AR model structure
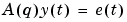
are estimated using variants of the least squares method.
The iddata object y contains the time-series data (just one output channel). The scalar n specifies the order of the model to be estimated (the number of A parameters in the AR model).
Note that the routine is for scalar time series only. For multivariate data use arx.
The estimate is returned in m and stored as an idpoly model. For the two lattice-based approaches, 'burg' and 'gl' (see below), the variable refl is returned containing the reflection coefficients in the first row, and the corresponding loss function values in the second. The first column is the zero-th order model, so that the (2,1) element of refl is the norm of the time series itself.
Variable approach allows you to choose an algorithm from a group of several popular techniques for computing the least-squares AR model. Available methods are as follows:
approach = 'fb': The forward-backward approach. This is the default approach. The sum of a least-squares criterion for a forward model and the analogous criterion for a time-reversed model is minimized.
approach = 'ls': The least-squares approach. The standard sum of squared forward prediction errors is minimized.
approach = 'yw': The Yule-Walker approach. The Yule-Walker equations, formed from sample covariances, are solved.
approach = 'burg': Burg's lattice-based method. The lattice filter equations are solved, using the harmonic mean of forward and backward squared prediction errors.
approach = 'gl': A geometric lattice approach. As in Burg's method, but the geometric mean is used instead of the harmonic one.
The computation of the covariance matrix can be suppressed in any of the above methods by ending the approach argument with 0 (zero), for example, 'burg0'.
Windowing, within the context of AR modeling, is a technique for dealing with the fact that information about past and future data is lacking. There are a number of variants available:
window = 'now': No windowing. This is the default value, except when approach = 'yw'. Only actually measured data are used to form the regression vectors. The summation in the criteria starts only at time n.
window = 'prw': Pre-windowing. Missing past data are replaced by zeros, so that the summation in the criteria can be started at time zero.
window = 'pow': Post-windowing. Missing end data are replaced by zeros, so that the summation can be extended to time N + n. (N being the number of observations.)
window = 'ppw': Pre- and post-windowing. This is used in the Yule-Walker approach.
The combinations of approaches and windowing have a variety of names. The least-squares approach with no windowing is also known as the covariance method. This is the same method that is used in the arx routine. The MATLAB default method, forward-backward with no windowing, is often called the modified covariance method. The Yule-Walker approach, least-squares plus pre- and post-windowing, is also known as the correlation method.
See Algorithm Properties for an explanation of the input argument maxsize.
Examples
Compare the spectral estimates of Burg's method with those found from the forward-backward nonwindowed method, given a sinusoid in noise signal.
y = sin([1:300]') + 0.5*randn(300,1);y = iddata(y);mb = ar(y,4,'burg');mfb = ar(y,4);bode(mb,mfb)
See Also
References
Marple, Jr., S. L. Digital Spectral Analysis with Applications, Prentice Hall, Englewood Cliffs, 1987, Chapter 8.
 | Algorithm Properties | armax |  |