| Fixed-Point Blockset | |
Division
As with multiplication, division with mismatched scaling is complicated. Mismatched division is permitted for simulation only. For code generation and bit-true simulation, the signals must all have zero biases and matched fractional slopes.
Fixed-Point Blockset Division Process
Consider the division of two numbers. Ideally, the real-world values obey the equation
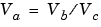
where Vb and Vc are the input values and Va is the output value. To see how the division is actually implemented, the three ideal values should be replaced by the general [Slope Bias] encoding scheme described in Scaling:
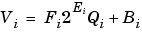
For the case where the slopes are one and the biases are zero for all signals, the solution of the resulting equation for the output stored integer, Qa, is given below:
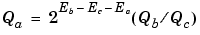
This equation involves an integer division and some bit shifts. If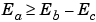 
, then any bit shifts are to the right and the implementation is simple. However, if 
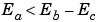, then the bit shifts are to the left and the implementation can be more complicated. The essential issue is the output has more precision than the integer division provides. To get full precision, a fractional division is needed. The C programming language provides access to integer division only for fixed-point data types. Depending on the size of the numerator, some of the fractional bits may be obtained by performing a shift prior to the integer division. In the worst case, it may be necessary to resort to repeated subtractions in software.
In general, division of values is an operation that should be avoided in fixed-point embedded systems. Division where the output has more precision than the integer division (i.e.,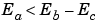 
) should be used with even greater reluctance. Division of signals with nonzero biases or mismatched slopes is not supported.
Example: The Division Process
Suppose you want to divide two numbers. Each of these numbers is represented by an 8-bit word, and each has a radix point-only scaling of 2-4. Additionally, the output is restricted to an 8-bit word with radix point-only scaling of 2-4.
The division of 9.1875 by 1.5000 is shown below.
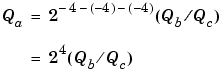
Assuming a large data type was available, this could be implemented as
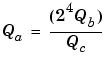
where the numerator uses the larger date type. If a larger data type was not available, integer division combined with four repeated subtractions would be used. Both approaches produce the same result, with the former being more efficient.
| | Multiplication | Shifts | |
